RANSAC算法进行误匹配对剔除原理

1. RANSAC基本思想

        在一组含有”外点”的数据中，不断迭代，最终正确估计出最优参数模型的算法。其中内点是符合最优参数模型的点，反之为外点。外点是一般指的数据中的噪声或无效点，比如说匹配中的误匹配和估计曲线中的离群点。所以也属于一种外点检测算法。

目的：为提高（点）特征的匹配率，提出剔除误匹配对，在特征匹配中，是为了寻找最佳的匹配模型。

1.1 算法步骤 

  1. 在样本N中随机采样K个点；
  2. 对这K个点进行模型拟合（这里的模型是什么模型？）；
  3. 计算其他点到该拟合模型的距离，并设置阈值，若大于阈值，为外点，则对该点进行舍弃，小于阈值，为内点，统计内点个数。阈值的设置为经验值，由具体应用和数据集决定；
  4. 然后以新的内点为基础，再次进行步骤2，得到新的拟合模型，迭代M次，选择内点数最多的模型，此时的模型为最优模型；
  5. 除此之外也可以在此基础上，选择出内点数最多的模型，然后对它进行重新估计，估计的时候可以采用最小二乘法来拟合。

1.2 迭代次数的公式

RANSAC算法中需要进行M次的迭代过程，且迭代的次数也是可以进行估算的。

        n数据中内点所占的比例（内点的概率p）：

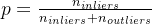
p=\frac{n_{inliers}}{n_{inliers}+n_{outliers}}

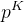        p^K是K个点都是内点的概率，选取的K个点至少有一个是外点的概率：

1-p^K

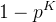
        因此就能得到迭代M次的情况下，选取点都是外点的概率，进而得到迭代M次中，至少有一次选取点k个点都是内点的概率，也就是正确模型的概率：z一般要求满足大于95%即可。

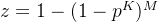
z=1-(1-p^K)^M

        最终得到迭代次数M

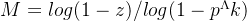
M = log(1-z)/log(1-p^{\Lambda}k)

2.举例（拟合最佳单应性矩阵）

"单应性矩阵"这个概念通常出现在计算机视觉和图像处理等领域，尤其是在处理图像投影变换时。在数学中，这个概念通常被称为"射影矩阵"或"射影变换"。

单应性矩阵是一个3x3的矩阵，用于描述二维投影变换，如旋转、缩放、剪切和透视等。它可以描述一个二维图像平面如何映射到另一个二维图像平面。这种映射保持了直线的直线性（也就是说，任何在原始图像中的直线在变换后的图像中仍然是直线），但不一定保持角度和长度。换句话说，图像中的线段可能在投影后的图像中扭曲或伸缩。

单应性矩阵H的一般形式如下：

H = [[h11, h12, h13], [h21, h22, h23], [h31, h32, 1]]

这里的hij代表矩阵中的元素，最后一个元素固定为1。矩阵中的其他元素定义了如何将一个二维坐标（x，y）映射到另一个二维坐标（x'，y'）：

[x', y', 1] = H * [x, y, 1]

其中x'和y'是变换后的坐标，*代表矩阵乘法。

在计算机视觉中，单应性矩阵通常用于矫正图像，使得从一个视角拍摄的图像可以被转换为从另一个视角拍摄的图像。例如，可以用单应性矩阵将一个倾斜的平面（如路面）的图像转换为从正上方观察的图像，这种技术通常用于车辆导航和无人驾驶等领域。

2.1 用RANSAC算法来寻找最佳单应性矩阵H

        在特征匹配中，我们最终要得到一个3*3的单应性矩阵。通常令h33=1来归一化矩阵，因此单应性矩阵有8个自由度h11-h32，求这八个未知数，至少要包含四个匹配点对。

s\left[\begin{array}{c}x'\\y'\\1\end{array}\right]=\left[\begin{array}{ccc}h_{11}&h_{12}&h_{13}\\h_{21}&h_{22}&h_{23}\\h_{31}&h_{32}&h_{33}\end{array}\right]\left[\begin{array}{c}x\\y\\1\end{array}\right]

        其中(x,y)表示目标图像角点位置,(x’,y’)为场景图像角点位置，s为尺度参数。

h33=1来归一化矩阵？
        H单应性矩阵，描述两个平面的映射关系，平面中点的坐标是二维的，第三维取1，为了简单化，将h33=1，为最简单的非零值，来归一化矩阵。

步骤：

  1. 通过SIFT算法已经进行了粗匹配，然后利用RANSAC算法来进精匹配；
  2. 首先在得到的匹配点中，随机选择4个匹配点对（不共线），其他匹配点为外点；
  3. 根据4对内点计算单应性矩阵；
  4. 根据此矩阵来测试其他匹配点(计算的是其他匹配点与该模型的投影误差），并设置阈值，若小于为新内点，若大于则为外点，也就是误匹配对，因此通过计算出的单应性矩阵，就能实现一次误匹配点的剔除；
  5. 将所有的内点统计进行内点更新，在此基础上再次进行步骤3，迭代M次，最终得到含有内点最多的模型，此时模型为最优模型，也就是我们最终所需要的单应性矩阵。
     

大体步骤确定后，我们还需要进行两个参数的确定，阈值和迭代次数。阈值一般是经验值，迭代次数根据上述迭代次数M公式计算得到。

如何用寻找到的单应性矩阵H来测试该模型下的其他匹配点？根据代价函数计算，代价函数最小的模型为最优模型。根据统计的内点数目，数目最多的为最优模型。

2.2 RANSAC 代码

3. 最小二乘法与RANSAC算法区别：

RANSAC算法：适用于含有较大的噪声或无效点的情况；

最小二乘法：适用于误差比较小的情况；

引入特征点对的误差能量来改进RANSAC，提升了算法运行效率和识别准确率。

优缺点：

        优点：当数据中有着大量的异常数据时，也能高精度的进行估计拟合

        缺点：对于异常数据超过50%的时候，拟合效果不佳。需要设置特定于问题的闽值。迭代次数若受到限制，那么达到迭代次数时拟合出来的模型可能并不是最佳模型。特定数据只能拟合出一个模型，一般多模型拟合采用霍夫变换。