详谈numpy.max,torch.max,argmax...

在编写或使用机器学习算法的过程中经常需要对numpy数组、tensor张量进行各种聚合操作，比如max，但是初次接触这块的东西，可能难以理解其中具体的聚合逻辑。

一。先上个简单的例子

给一个3行4列的numpy数组，按第0维取最大值。

e6eca3736aee498ca717e26eb37153a6.png

import numpy as np
import numpy.random

np.random.seed(0)
a = np.random.randint(0, 100, (3, 4), dtype=np.int32)
print(f'a:\r\n{a}')
a_max_x = a.max(axis=0)
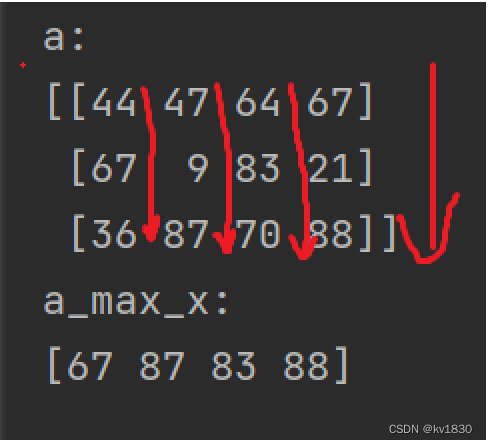
print(f'a_max_x:\r\n{a_max_x}')

按第0维，即指定axis=0。这到底是啥意思呢，直接来个简单的图，就是竖着计算啦，所以就是第0列取个最大值，第1列取个最大值，第2列最个最大值，第3列取个最大值。最终得到的是一行4列的结果。

1beb50e639e04800aec9b239e380a029.png

那我要是按第1维呢，即改成axis=1，那就是横着取啦，第0行取个最大值，第1行。。。，第2行。。。

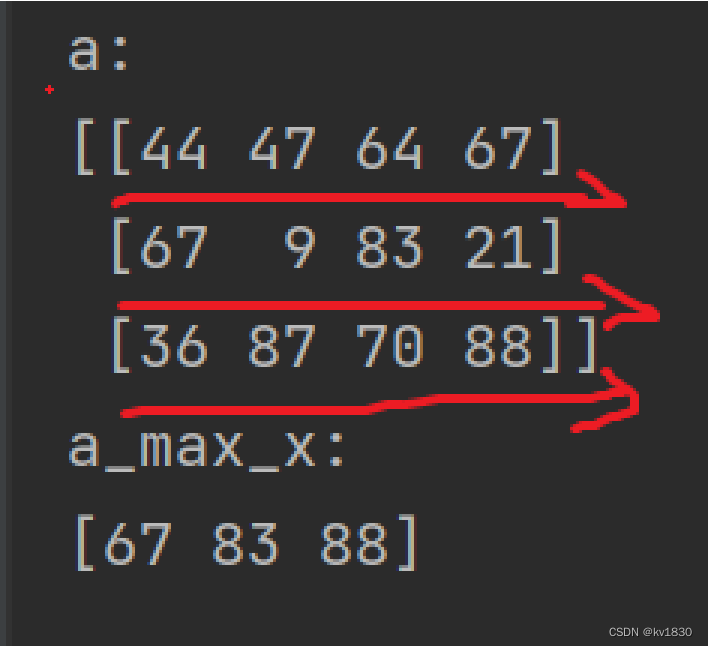
a6388f6f82b44310b3ab5b1288e8c5e2.png

也就是说按第0维就是竖着取，按第1维就是横着取。好像蛮奇怪的哦，但是也好记，死背！

等等，先别划走，我要是这么说就完了，那就不叫详谈了！

二。再来个难点的例子

二维的数组确实能硬背，但来个三维的呢？现在是2行3列4垂（我瞎起个维度的名字）

import numpy as np
import numpy.random

np.random.seed(0)
a = np.random.randint(0, 100, (2, 3, 4), dtype=np.int32)
print(f'a:\r\n{a}')
a_max_x = a.max(axis=0)
print(f'a_max_x:\r\n{a_max_x}')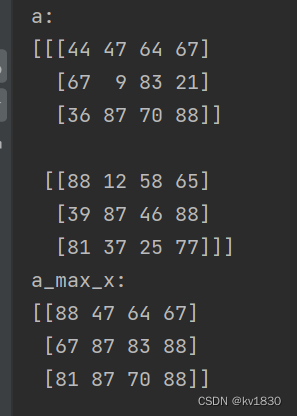

57712342892d45d8bd7eef64ac1a665d.png

这箭头怎么画？箭头是不太好画了，因为有3个维度，但现在用平面来展示数据，没法在这其中画出1个维度的箭头了，但是下面的红线两连的一组组数据，就是做聚合的一组组数据。

2行3列4垂，现在按第0维聚合，所以是两两聚合（听不懂没关系，下面有更容易懂的）

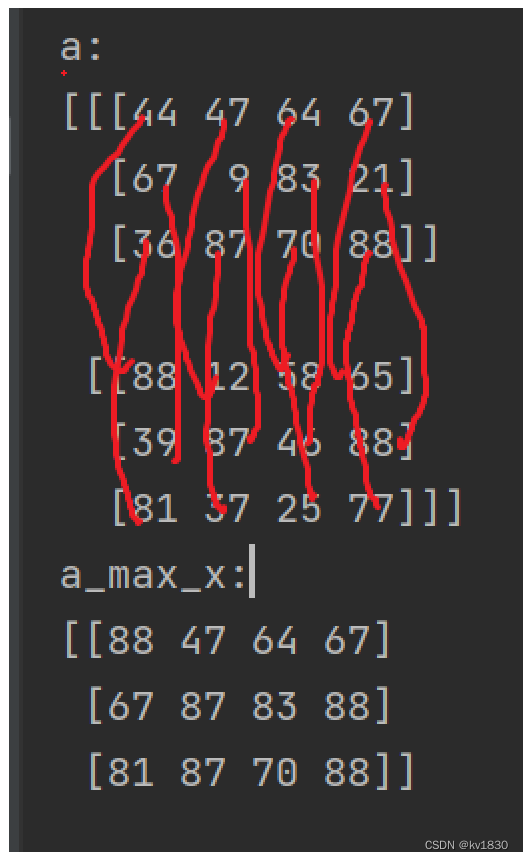
cb18b6f06bbb4866aab21e454f7e1240.png

如果上面的弄明白了，那直接跳跃一下，argmax的结果又是什么情况？

import numpy as np
import numpy.random

np.random.seed(0)
a = np.random.randint(0, 100, (2, 3, 4), dtype=np.int32)
print(f'a:\r\n{a}')
a_max_x = a.max(axis=0)
print(f'a_max_x:\r\n{a_max_x}')
a_max_x_arg = a.argmax(axis=0)
print(f'a_max_x_arg:\r\n{a_max_x_arg}')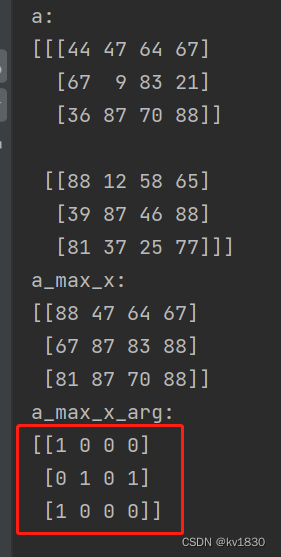

e9b6db98578046af91fe0a6099c0e0cf.png

红框里的是个啥玩意儿？这东西有什么用？莫急，其实如果真弄明白了聚合逻辑，就会知道这东西是什么，怎么用了。

三。具体的聚合逻辑

1.二维数组聚合

还是先从简单的3行4列入数，具体来讲讲它的聚合逻辑。按第0维聚合，其实就是沿着第0维把多个数聚合成1个，注意，这是有条件的，即第0维度的下标可变，其它维度下标不变，得到多个值，把这多个值聚合成一个值。

设第0维的坐标叫x，第1维的坐标叫y。那就是在

y固定为0时，取x为0，1，2得到3个值，求最大值

y固定为1时，取x为0，1，2得到3个值，求最大值

y固定为2时，取x为0，1，2得到3个值，求最大值

y固定为3时，取x为0，1，2得到3个值，求最大值

如下图 。

7df5809f11f64f1fafbd1a9e7a00b8df.png

如果让你写两层循环来实现聚合，y应该是外循环变量，x是内循环变量。最终得到的是1行4列的4个值（其实最后已经没有行这个维度了，因为它聚合成一个值了，二维的东西会聚合成一维，三维的东西会聚合成二维）

同理如果是延第1维聚合，就是如下图：

03612c6b80f84030887cda10ae27e803.png

最终得到三行一列的3个值（其实已经没有列这个维度了）

这里插一句，如果我仍然想保留列这个维度呢？只要把keepdims指定为True就行了（默认是False）

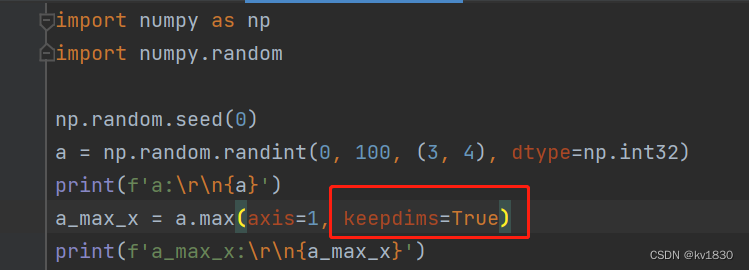
8db12e7f75b14168b004d2c033d11313.png

可以看到结果仍然是二维的

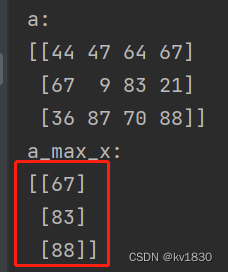
b01b7de6ba7a45d7bcb6ad7f665e2a35.png

2.那argmax的结果又是啥呢？

还是3行4列，按第0维聚合，现在看argmax的结果，再贴一下代码，现在主要看的是a_max_x_arg = a.argmax(axis=0)

import numpy as np
import numpy.random

np.random.seed(0)
a = np.random.randint(0, 100, (3, 4), dtype=np.int32)
print(f'a:\r\n{a}')
a_max_x = a.max(axis=0)
print(f'a_max_x:\r\n{a_max_x}')
a_max_x_arg = a.argmax(axis=0)
print(f'a_max_x_arg:\r\n{a_max_x_arg}')

其结果就是如下图，每次聚合的时候，到底最大的那个值的x值（即第0维的坐标）是多少（而max是直接求出最大的元素值，而非坐标值）

3e73b4dbc37a46fa9687543f4c36fe50.png

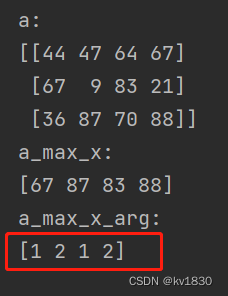
8948871439104a2aa60a949ab4baf6f0.png

注意这里x值是从0开始算的。

这个结果有什么用呢？这个结果可以作用在原数组上，求出聚合值。

(1)先来个最最简单的，原数组就是1维的

import numpy as np
import numpy.random

np.random.seed(0)
a = np.random.randint(0, 100, (3,), dtype=np.int32)
print(f'a:\r\n{a}')
a_max_x = a.max(axis=0)
print(f'a_max_x:\r\n{a_max_x}')
a_max_x_arg = a.argmax(axis=0)
print(f'a_max_x_arg:\r\n{a_max_x_arg}')
another_a_max_x = a[a_max_x_arg]
print(f'有点绕的a_max_x:\r\n{another_a_max_x}')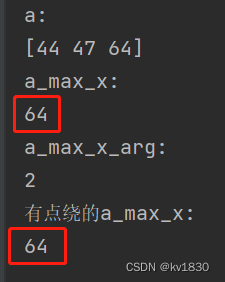

343350ad215541f0bd1df18700b0f6c6.png

由于是一维的，这里求出的最大值下标(a_max_x_arg)就是一个标量，因为只有一个值。那直接用a[a_max_x_arg]就能求出最大值啦，如上图，红框的两个值是一样的，只是后者多绕了一步。

你可能会问，我既然能直接求出最大值，我干麻还先求个下标，再用它去取最大值？

因为有的时候你会有多个数组，比如一个是成绩数组，一个是学号数组或者学生名字数组（numpy数组的类型也可以是字符串哦），我不但要求出最高的成绩，我还想知道它对应的学号或者名字，这个时候你就得先求下标，再求成绩和学号。

(2)二维的

import numpy as np
import numpy.random

np.random.seed(0)
a = np.random.randint(0, 100, (3, 4), dtype=np.int32)
print(f'a:\r\n{a}')
a_max_x = a.max(axis=0)
print(f'a_max_x:\r\n{a_max_x}')
a_max_x_arg = a.argmax(axis=0)
print(f'a_max_x_arg:\r\n{a_max_x_arg}')
another_a_max_x = a[a_max_x_arg, range(4)]
print(f'有点绕的a_max_x:\r\n{another_a_max_x}')

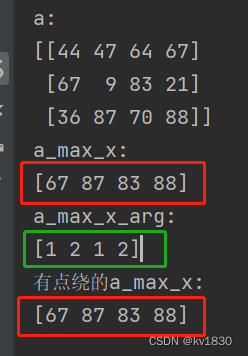
ecb64b48b3eb4cc2987e796d2ff8b10b.png

如上图，红框就是直接求出的最大值与间接求出的最大值，绿框就是4个最大值的下标x，它们分别对应的y是几呢，肯定是0、1、2、3啊，还记得吗，y是外层循环啊，每个y值都会遍历一遍。所以argmax的结果没必要再给你返回y，毫无悬念的多余信息不会返回给你！

4个x与4个y的对应关系如下图。

71b1c89ff4844022b64fdedab79980a8.png

所以在原数组上取最大值的时候，自然就是用a[a_max_x_arg, range(4)]这种形式来取，0维、1维分别是一个序列，它的意思就是在原数组上分别取出(x=1,y=0),(x=2,y=1),(x=1,y=2),(x=2,y=3)的4个值。

(3)三维的

先等下，三维的最大值是怎么取的还没讲呢

3.三维数组的聚合逻辑

import numpy as np
import numpy.random

np.random.seed(0)
a = np.random.randint(0, 100, (2, 3, 4), dtype=np.int32)
print(f'a:\r\n{a}')
a_max_x = a.max(axis=0)
print(f'a_max_x:\r\n{a_max_x}')

其实如果二维数组的聚合逻辑理解了，更多维度的也就理解了，还是那句话，固定其它维度，在单一维度上做聚合。所以如果是三维数组，在第0维(x轴)聚合，那就是每次都固定1维(y轴)、2维(z轴)，取x轴上的多个值，求最大值。

此时如果用代码循环来求结果，需要3层循环，外面两层是y轴、z轴（谁先谁后无所谓），最内层是x轴。

ce2022e3de05458584e0c48a3e052b01.png

图1

示例如上图。最终聚合出来的就是保留y、z两个维度的二维数组了。

如果是按第1维聚合，那就是每次固定0维(x)，2维(z)，取第1维(y)的多个值做聚合。

4.三维的argmax结果怎么用呢？

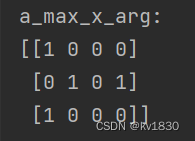
e93ba2af621944c08a6b08ba2253b734.png

图2

如图2是2行3列4垂的三维数组按第0维聚合得到的argmax结果，如果二维的argmax想明白了，三维的聚合逻辑也想明白了，那就会知道，这里的argmax结果中指的全是第0维的坐标值（即x值），那它们对应的y、z是多少？其实y就是这个二维数组的第0维的下标、z就是这个二维数组的第1维的下标。如果觉得有点绕，把三维数组聚合逻辑中的图1再看看。

接下来怎么用这个结果去原数组上取出聚合结果呢？

a[a_max_x_arg, range(3), range(4)] 这样行不行？

肯定不行，因为这3个东西的形状不一样啊。如果3个都是1维序列（假设长度为都是3），那可以，含义就是我要从3维数组里取3个值，我分别告诉你这3个值的x、y、z下标是多少。

import numpy as np
import numpy.random

np.random.seed(0)
a = np.random.randint(0, 100, (2, 3, 4), dtype=np.int32)
print(f'a:\r\n{a}')
print(a[[0, 0, 0], range(3), range(3)])

比如如上代码，取的就是下图中红框中的值

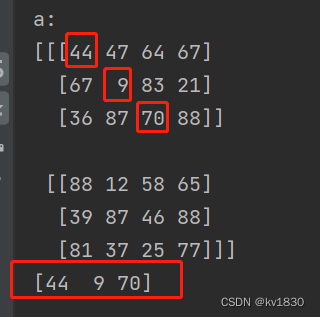
现在回到之前的场景，argmax给我返回的是在所有的y、z上聚合出的结果的x值，即a_max_x_arg，它是一个二维的数组，你用它去索引原数组的时候，那对应的y、z也得是同样的形状才行啊，即是相同形状的二维数组，并且其中的每个值都是与x相对应的。y、z的值如下。结合上面的聚合逻辑想一想，是不是这样。

代码中怎么用呢，直接用a[a_max_x_arg, np.arange(3)[:, None], np.arange(4)]就行啦，这里是利用了广播机制，它们两广播后就会变成上面的样子。

import numpy as np
import numpy.random

np.random.seed(0)
a = np.random.randint(0, 100, (2, 3, 4), dtype=np.int32)
print(f'a:\r\n{a}')
a_max_x = a.max(axis=0)
print(f'a_max_x:\r\n{a_max_x}')
a_max_x_arg = a.argmax(axis=0)
print(f'a_max_x_arg:\r\n{a_max_x_arg}')

another_a_max_x = a[a_max_x_arg, np.arange(3)[:, None], np.arange(4)]
print(f'有点绕的a_max_x:\r\n{another_a_max_x}')

完整代码如上。

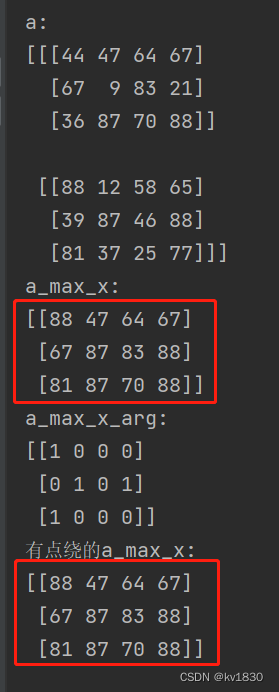
索引后取到的最大值与直接计算的最大值是一样的吧！

四。举个生动点的例子

接下来举一个更实际的例子，可以自已检验一下到底理解了没有，空讲x、y、z三个维度太抽象啦，还是2行3列4垂，但是给它赋予具体的含义。

现在有2个班级，每个班级有3组，每组有4个学生（小班化教学~~），现在有一个三维数组，存的就是这些学生的考试成绩，所以就是2行3列4垂的数组了。

现在要淘汰学生，按某维度聚合，只保留成绩最高的学生。

问题1：如果按第0维聚合，最终得到的是什么结果？有几个班级？几个组？每组几个学生？

结果就是只有一个班级啦（其实班级维度已经没了，还记得吗，除非加上keepdims=True），仍然是3组，每组4个学生。想一想，具体是怎么两两淘汰的，印象会更深刻哦。

问题2：如果现在的淘汰要求是，每班只留下成绩最高的学生，其余的全淘汰！应该按哪个维度聚合？

给你挖了个坑哈哈，延单一维度无法聚合出这个结果啊，因为你需要把第1维（y）、第2维（z）全聚合了才行。具体做法可以有多种啦，比如分两次聚合，或者先把数组reshape成2行12列，然后按第1维聚合。

五。torch的max

上面讲的都是numpy，那pytorch呢？其实是一样的啊，顶多是函数名、参数啥的有点区别，比如pytorch的维度参数名不叫axis，叫dim。至于聚合时保留原维度，同样也叫keepdims。

直接上一个示例

import torch
torch.random.manual_seed(0)
a = torch.randint(0, 100, (3, 4), dtype=torch.int32)
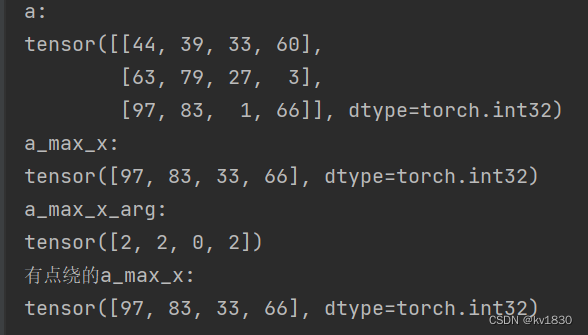
a_max_x, a_max_x_arg = a.max(dim=0)
print(f'a:\r\n{a}')
print(f'a_max_x:\r\n{a_max_x}')
print(f'a_max_x_arg:\r\n{a_max_x_arg}')
another_a_max_x = a[a_max_x_arg, range(4)]
print(f'有点绕的a_max_x:\r\n{another_a_max_x}')

59fdbb04b05b41c8b672f84428421270.png