GNSS卫星姿态解算

        GNSS卫星姿态影响太阳光压辐射力的建模与卫星天线改正，正确解算卫星姿态是GNSS数据解算中的关键步骤。

        卫星的姿态指卫星的星体坐标轴XYZ在惯性系下的指向，其中Z轴始终指向地球地心，Y轴为卫星太阳能帆板的旋转轴，它始终与太阳-卫星方向垂直（为了最大程度地利用太阳辐射能量）。当然，Y轴同时也垂直于Z轴，最后的X轴与Y轴和Z轴组成右手坐标系。卫星、地球和太阳三者间的几何关系可见下图：

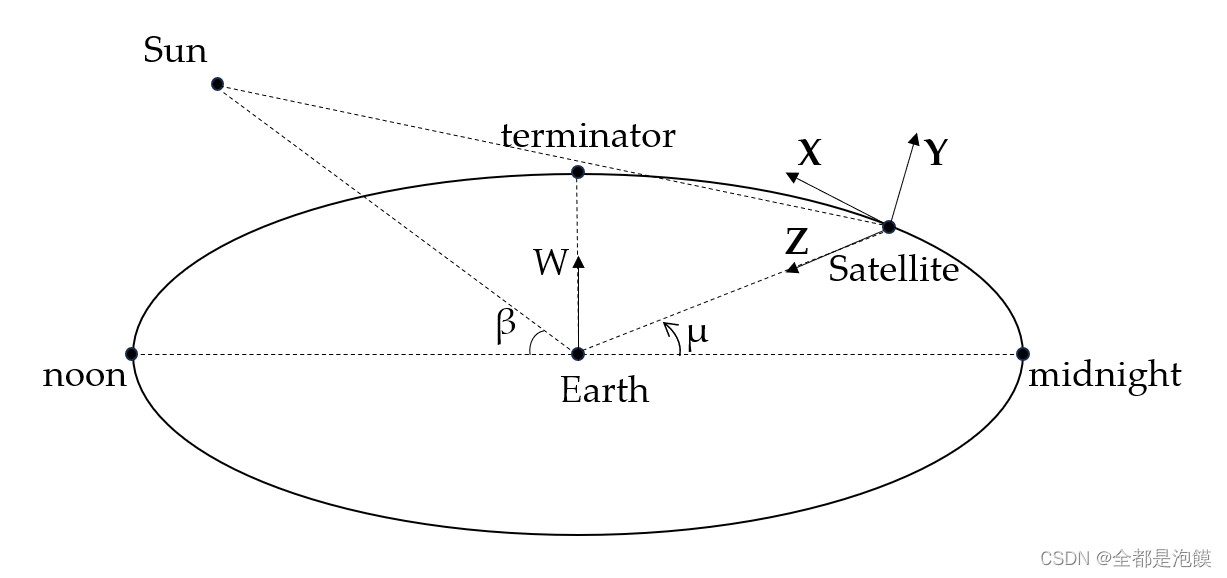
         在非地影期的数据解算过程中，我们已知惯性系下的太阳位置向量xsun，卫星位置向量xsat，卫星速度向量vsat。那么便可以直接求得卫星的Z轴，

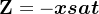
        卫星指向太阳的向量为Sc2sun，

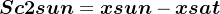
        根据Sc2sun与xsat，可以叉乘求得卫星的Y轴，

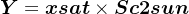
        最后由XZ轴可以算得卫星的X轴，

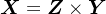
        以上是卫星在非地影期间的姿态解算，然而在卫星地影期间则需考虑更多因素，首先需要求解太阳高度角β与卫星轨道角μ，其中β可以由轨道面法向向量W与xsun求得，

 

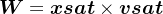
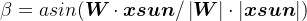
        求解卫星轨道角μ则略微复杂些，首先需要求得地球指向午夜点的向量midnight,

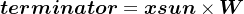
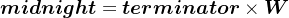
        之后便可根据midnight与xsat算得轨道角μ了，

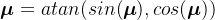
        其中，

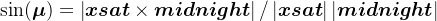
        由于向量的模等于向量点乘自身的单位向量tmpunit，因此

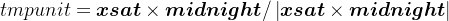
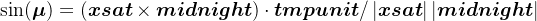
        同时容易得到

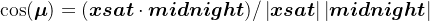
        因此，最后得到轨道角μ，其取值范围为-pai到pai

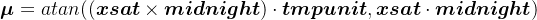
        由β与μ即可判断卫星是否处于地影期，最后根据不同卫星系统的地影期姿态控制模式解算得到具体姿态。