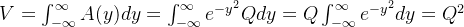第三单元 用python学习微积分（二十三）第三单元总结（下）-- 切面法求体积

本文内容来自于学习麻省理工学院公开课：单变量微积分-第三次考试复习-网易公开课

开发环境准备：CSDN

目录

二、刨切

1、回顾

2、老师这节课说的问题， 是用切片法求​对z轴旋转形成的体的体积。

二、刨切

回顾Bullseye：第三单元 用python学习微积分（二十二）功、平均值、概率（下）和 数值积分 (1)

中的概率问题

1、回顾

概率的经典问题，投飞标问题， 问如果一个人向靶心投飞镖，击中的次数与 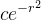ce^{-r^2} (c是常数,假设为1)成正比，

有多大的概率会射到靶子旁边的人。至于这个计算有没有实际意义呢？这里老师提到，二战时有人研究德国的V-2导弹瞄准伦敦发射，会击中哪里，用的就是这个函数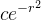ce^{-r^2} （结果相近！）。

这里击中的概率与距离靶心的长度 r 相关，类正态分布

V = \int_{r_1}^{r_2} 2\pi r \times (ce^{-r^2}) dr = -c\pi e^{-r^2}|_{0}^{\infty} = c\pi( e^{-r_1^2} - e^{-r_2^2} )

2、老师这节课说的问题， 是用切片法求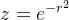z = e^{-r^2}对z轴旋转形成的体的体积。

​

老师这里预设了一个常量

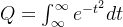
Q = \int_{\infty}^{\infty} e^{-t^2}dt

用旋转法画出这个体

from sympy import *
import numpy as np
import matplotlib.pyplot as plt
import numpy as np
from enum import Enum
from itertools import product, combinations

from matplotlib import cm
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection, Line3DCollection
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(12, 12),
                facecolor='lightyellow'
                )
# draw sphere
ax = fig.gca(fc='whitesmoke',
              projection='3d' 
           )
 
class EnumAxis(Enum):
    XAxis = 1
    YAxis = 2
    ZAxis = 3
    
def fromXYZM(xyzM):
    ret = []
    
    m=range(0,xyzM.shape[0])
    
    for b in zip(m,[0]):
        ret.append((xyzM[b]))
    for b in zip(m,[1]):
        ret.append((xyzM[b]))
    for b in zip(m,[2]):
        ret.append((xyzM[b]))
    return ret

def plot_surface(x, y, z, dx, dy, dz, ax):
    xx = np.linspace(x, x+dx, 2)
    yy = np.linspace(y, y+dy, 2)
    zz = np.linspace(z, z+dz, 2)
    
    if(dz == 0):
        xx, yy = np.meshgrid(xx, yy)
        ax.plot_surface(xx, yy, z, alpha=0.25)
    
    if(dx == 0):
        yy, zz = np.meshgrid(yy, zz)
        ax.plot_surface(x, yy, zz, alpha=0.25)
    
    if(dy == 0):
        xx, zz = np.meshgrid(xx, zz)
        ax.plot_surface(xx, y, zz, alpha=0.25)
    

def plot_opaque_cube(x, y, z, dx, dy, dz, ax):

    xx = np.linspace(x, x+dx, 2)
    yy = np.linspace(y, y+dy, 2)
    zz = np.linspace(z, z+dz, 2)

    xx, yy = np.meshgrid(xx, yy)
    ax.plot_surface(xx, yy, z)
    ax.plot_surface(xx, yy, z+dz)

    yy, zz = np.meshgrid(yy, zz)
    ax.plot_surface(x, yy, zz)
    ax.plot_surface(x+dx, yy, zz)

    xx, zz = np.meshgrid(xx, zz)
    ax.plot_surface(xx, y, zz)
    ax.plot_surface(xx, y+dy, zz)
    # ax.set_xlim3d(-dx, dx*2, 20)
    # ax.set_xlim3d(-dx, dx*2, 20)
    # ax.set_xlim3d(-dx, dx*2, 20)
    
def DrawAxis(ax, xMax, yMax, zMax):
    # 设置坐标轴标题和刻度
    ax.set(xlabel='X',
           ylabel='Y',
           zlabel='Z',
           xticks=np.arange(-xMax, xMax, 1),
           yticks=np.arange(-yMax, yMax, 1),
           zticks=np.arange(-zMax, zMax, 1)
          )

    ax.plot3D(xs=[xMax,-xMax, 0,0, 0, 0, 0,0, ],    # x 轴坐标
              ys=[0, 0,0, yMax,-yMax, 0, 0,0, ],    # y 轴坐标
              zs=[0, 0,0, 0,0, 0, zMax,-zMax ],    # z 轴坐标
              zdir='z',    # 
              c='k',    # color
              marker='o',    # 标记点符号
              mfc='r',    # marker facecolor
              mec='g',    # marker edgecolor
              ms=10,    # size
            )

def Rx(x,y,z,theta):
    A = [x,y,z] * np.matrix([[ 1, 0           , 0           ],
                   [ 0, cos(theta),-sin(theta)],
                   [ 0, sin(theta), cos(theta)]])
    return fromXYZM(A)
 
def Ry(x,y,z,theta):
    A = [x,y,z] * np.matrix([[ cos(theta), 0, sin(theta)],
                   [ 0           , 1, 0           ],
                   [-sin(theta), 0, cos(theta)]])
    return fromXYZM(A)
 
def Rz(x,y,z,theta):
    A = [x,y,z] * np.matrix([[ cos(theta), -sin(theta), 0 ],
                   [ sin(theta), cos(theta) , 0 ],
                   [ 0           , 0            , 1 ]])
    return fromXYZM(A)

def Equal(a, b, tol):
    if(abs(a - b) < tol):
        return true
    return false

def GetValuesByIdxMGrid(grid, idx):
    length = int(len(idx)/2)
    values = []
    for n in range(length):
        i = idx[2*n]
        j = idx[2*n+1]
        values.append(grid[i][j])
    return values
        
def FindIndexInMGrid(grid, value, tol):
    idx = []
    values = []
    for i in range(len(grid)):
        for j in range(len(grid[i])):
            if(Equal(grid[i][j], value, tol)):
                idx.append(i)
                idx.append(j)
                values.append(value)
                
    return idx,values
            
def MakeSliceByAxis(xarr, yarr, zarr, axis, value, tol):
    idx = []
    xret = []
    yret = []
    zret = []
    if axis == EnumAxis.XAxis:
        idx,xret = FindIndexInMGrid(xarr, value,tol)
        yret = GetValuesByIdxMGrid(yarr, idx)
        zret = GetValuesByIdxMGrid(zarr, idx)
    else:
        if axis == EnumAxis.YAxis:
            idx,yret = FindIndexInMGrid(yarr, value,tol)
            xret = GetValuesByIdxMGrid(xarr, idx)
            zret = GetValuesByIdxMGrid(zarr, idx)
        else:
            idx,zret = FindIndexInMGrid(zarr, value,tol)
            xret = GetValuesByIdxMGrid(xarr, idx)
            yret = GetValuesByIdxMGrid(yarr, idx)
            
            
    return np.array(xret),np.array(yret),np.array(zret)
    
    
def MakeRotateByAxisS(xFrom,xTo,steps,expr,thetaFrom,thetaTo,thetaSteps, rotatedBy):
    stepsArr = np.linspace(thetaFrom ,thetaTo, thetaSteps)
    xarr = []
    yarr = []
    zarr = []
    i = 0
    for theta in stepsArr:
        x,y,z = MakeRotateByAxis(xFrom,xTo,steps,expr,theta,rotatedBy)
        xarr.insert(i, x)
        yarr.insert(i, y)
        zarr.insert(i, z)
        i = i + 1
    
    return np.array(xarr), np.array(yarr), np.array(zarr)

def MakeRotateByAxis(xFrom,xTo,steps,expr,theta,rotatedBy):
    yarr = []
    xarr = np.linspace(xFrom ,xTo, steps) 
    xyz = []
    xx = []
    yy = []
    zz = []
    for xval in xarr:
        yval = expr.subs(x,xval)
        if rotatedBy == EnumAxis.XAxis:
            xyz =  Rx(xval,yval,0,theta)
        elif rotatedBy == EnumAxis.YAxis:
            xyz =  Ry(xval,yval,0,theta)
        else:
            xyz =  Rz(xval,yval,0,theta)
            
        xx.append(float(xyz[0])) #using float() to prevent isnan issue
        yy.append(float(xyz[1]))
        zz.append(float(xyz[2]))
        #if(np.isnan(float(xyz[2]))):
            #zz.append(float(0.0))
        #else:
            #zz.append(xyz[2])
    return xx,yy,zz
    
def RotateByAxis(xFrom,xTo,steps,expr,theta,color,ax,rotatedBy):
    xx,yy,zz = MakeRotateByAxis(xFrom,xTo,steps,expr,theta,rotatedBy)
    ax.plot(xx, yy, zz, color)
    
def DrawXY(xFrom,xTo,steps,expr,color,label,plt):
    yarr = []
    xarr = np.linspace(xFrom ,xTo, steps) 
    for xval in xarr:
        yval = expr.subs(x,xval)
        yarr.append(yval)
    y_nparr = np.array(yarr) 
    plt.plot(xarr, y_nparr, c=color, label=label)    
    #zarr = xarr*0 +1
    #plt.plot(xarr, y_nparr,zarr, c=color, label=label)    

def DrawInt(xFrom,xTo,steps,expr,color,plt, label=''):
    if(xFrom < 0 and xTo < 0):
        DrawIntNegative(xFrom,xTo,steps,expr,color,plt, label)
    else:
        if(xFrom > 0 and xTo > 0):
            DrawIntPostive(xFrom,xTo,steps,expr,color,plt, label)
        else:
            DrawIntNegative(xFrom,0,steps,expr,color,plt, label)
            DrawIntPostive(0,xTo,steps,expr,color,plt, label)
    
def DrawIntNegative(xFrom1,xTo1,steps,expr,color,plt, label=''):
    xFrom = 0 - xTo1
    xTo = 0 - xFrom1
    width = (xTo - xFrom)/steps
    xarr = []
    yarr = []
    area = 0
    xprev = xFrom
    yvalAll =  0
    xarr.append(0)
    yarr.append(0)
    for step in range(steps):
        yval = expr.subs(x,xprev)
        area += width * yval
        xarr.append(0-xprev)
        yarr.append(0-area)
        xprev= xprev + width
    plt.plot(xarr, yarr, c=color, label =label)

def plot_surface(x, y, z, dx, dy, dz, ax, paraAlpha):
    xx = np.linspace(x, x+dx, 2)
    yy = np.linspace(y, y+dy, 2)
    zz = np.linspace(z, z+dz, 2)
    
    if(dz == 0):
        xx, yy = np.meshgrid(xx, yy)
        ax.plot_surface(xx, yy, z, alpha=paraAlpha)
    
    if(dx == 0):
        yy, zz = np.meshgrid(yy, zz)
        ax.plot_surface(x, yy, zz, alpha=paraAlpha)
    
    if(dy == 0):
        xx, zz = np.meshgrid(xx, zz)
        ax.plot_surface(xx, y, zz, alpha=paraAlpha)
    
def DrawIntPostive(xFrom,xTo,steps,expr,color,plt, label=''):
    width = (xTo - xFrom)/steps
    xarr = []
    yarr = []
    area = 0
    xprev = xFrom
    yvalAll =  0
    xarr.append(0)
    yarr.append(0)
    for step in range(steps):
        yval = expr.subs(x,xprev)
        area += width * yval
        xarr.append(xprev)
        yarr.append(area)
        xprev= xprev + width
    plt.plot(xarr, yarr, c=color, label =label)    
        
def DrawRects(xFrom,xTo,steps,expr,color,plt, label=''):
    width = (xTo - xFrom)/steps
    xarrRect = []
    yarrRect = []
    area = 0
    xprev = xFrom
    yvalAll =  0
    for step in range(steps):
        yval = expr.subs(x,xprev + width)
        xarrRect.append(xprev)
        xarrRect.append(xprev)
        xarrRect.append(xprev + width)
        xarrRect.append(xprev + width)
        xarrRect.append(xprev)
        yarrRect.append(0)
        yarrRect.append(yval)
        yarrRect.append(yval)
        yarrRect.append(0)
        yarrRect.append(0)
        area += width * yval
        plt.plot(xarrRect, yarrRect, c=color)    
        xprev= xprev + width
        yvalAll += yval
    print('============================')    
    if len(label)!=0:
        print(label)    
    print('============================')
    print('width = ', width)
    print('ave = ', yvalAll / steps)
    print('area = ',area)
    areaFinal = (integrate(expr, (x,xFrom,xTo)))
    print ('area final = ',areaFinal)
    print ('ave final = ', areaFinal / (xTo - xFrom))

def TangentLine(exprY,x0Val,xVal):
    diffExpr = diff(exprY)
    x1,y1,xo,yo = symbols('x1 y1 xo yo')
    expr = (y1-yo)/(x1-xo) - diffExpr.subs(x,x0Val)
    eq = expr.subs(xo,x0Val).subs(x1,xVal).subs(yo,exprY.subs(x,x0Val))
    eq1 = Eq(eq,0)
    solveY = solve(eq1)
    return xVal,solveY

def DrawTangentLine(exprY, x0Val,xVal1, xVal2, clr, txt):
    x1,y1 = TangentLine(exprY, x0Val, xVal1)
    x2,y2 = TangentLine(exprY, x0Val, xVal2)
    plt.plot([x1,x2],[y1,y2], color = clr, label=txt)
    
def Newton(expr, x0):
    ret = x0 - expr.subs(x, x0)/ expr.diff().subs(x,x0)
    return ret

def GridToArray(xx,yy,zz):
    ret = []
    length = len(xx)
    n = 0
    for i in range(length):
        length1 = len(xx[i])
        for j in range(length1):
            coordinate = []
            coordinate.append(xx[i][j])
            coordinate.append(yy[i][j])
            coordinate.append(zz[i][j])
            ret.insert(n, coordinate)
            n += 1
    return np.array(ret) 
                   
def DrawExpressionZSliceFixedY(xFrom,xTo,steps, fixedY, zBottomValue, ExprToCalZ, color, gca):
    b= fixedY
    xarr = np.linspace(xFrom,xTo, steps)
    yarr = b

    X,Y = np.meshgrid(xarr,yarr)

    Z = ExprToCalZ(X,Y)

    z0 = zBottomValue

    xx = X.tolist()
    xx.insert(1, X[0].tolist())
    X = np.array(xx)
    yy = Y.tolist()
    yy.insert(1, Y[0].tolist())
    Y = np.array(yy)
    zz = Z.tolist()
    zz.insert(1, ((Z[0]**0)*z0).tolist())
    Z = np.array(zz)
    #ax.plot_wireframe(X,Y,Z)
    gca.plot_surface(X,Y,Z, color = color, alpha=0.5)


DrawAxis(ax, 5,5,5)

x = symbols('x')
expr = np.e**(-x**2)
xx,zz,yy = MakeRotateByAxisS(0,3,50,expr,0.0,2*np.pi,50, EnumAxis.YAxis)
points = GridToArray(xx,yy,zz)
ax.plot_surface(xx,yy,zz)
ax.view_init(elev=10,    # 仰角
             azim=110    # 方位角
            )
plt.show()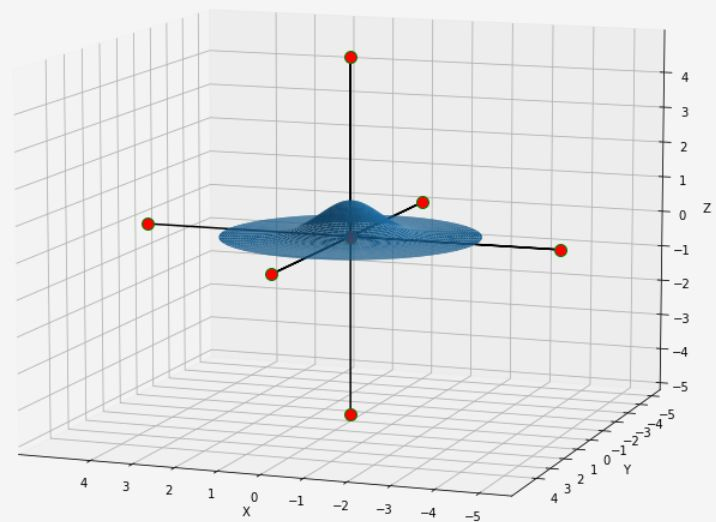

​做4个切片：

fig = plt.figure(figsize=(12, 12),
                facecolor='lightyellow'
                )
# draw sphere
ax = fig.gca(fc='whitesmoke',
              projection='3d' 
           )
DrawAxis(ax, 1.5,1.5,1.5)

def exprZ(xPara,yPara):
    return np.e**(-(xPara**2+yPara**2))

b= 1.2
DrawExpressionZSliceFixedY (-3,3,50,b,exprZ(3,b),exprZ,'b',ax)
b= 1.0
DrawExpressionZSliceFixedY (-3,3,50,b,exprZ(3,b),exprZ,'b', ax)
b= 0.8
DrawExpressionZSliceFixedY (-3,3,50,b,exprZ(3,b),exprZ,'b', ax)
b= 0.0
DrawExpressionZSliceFixedY (-3,3,50,b,exprZ(3,b),exprZ,'b', ax)

ax.view_init(elev=10,    # 仰角
             azim=130    # 方位角
            )
plt.show()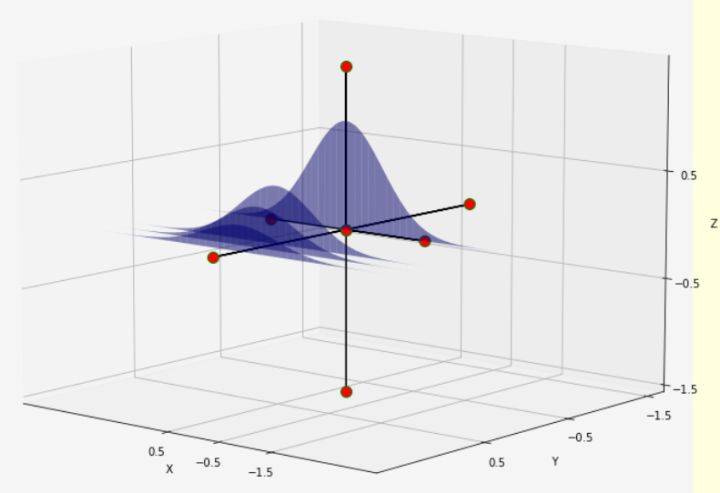

​上面蓝色帽子似的体的体积其实是 {每一片切片的面积乘以切片厚度} 的累加。

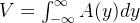
V = \int_{-\infty}^{\infty} A(y)dy

当y=b（1.5）时， ｚ是？

b = 1.5
x = symbols('x')
expr = x**0*b

DrawXY (-5,5,50,expr,color='b',label = 'y=b',plt = plt)

plt.plot([0,2.4], [0,b], c='r', label='r')
plt.plot([0,2.4], [0,0], c='black', label='x')
plt.plot([2.4,2.4], [0,b], c='green', label='y')
plt.plot(2.4,b,lw=0, marker='o', fillstyle='none',label='point on (y=b)')
plt.legend(loc='upper left')
plt.show()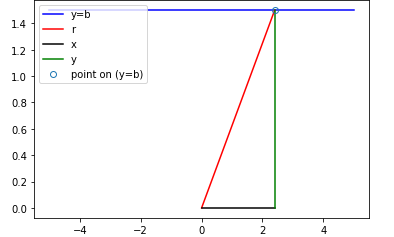

​

计算A(b), 即 y = b 时的图形切片的面积

这里考虑

z = e^{-r^2}

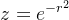
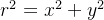
r^2 = x^2 + y^2

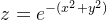
z = e^{-(x^2+y^2)}

y = b

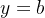
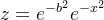
z = e^{-b^2} e^{-x^2}

可以看出 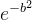e^{-b^2} 是一个常数，z的高度的变化随x， 而把所有的高为z、宽为dx的矩形的面积累加即是A(b)的值

前提条件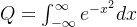： Q = \int_{-\infty}^{\infty} e^{-x^2} dx

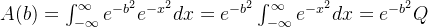A(b) = \int_{-\infty}^{\infty} e^{-b^2} e^{-x^2}dx = e^{-b^2}\int_{-\infty}^{\infty} e^{-x^2}dx = e^{-b^2}Q ｛这里ｙ不随ｘ变化而变化，所以这个ｙ＝ｂ可以看作是常数｝

V = \int_{-\infty}^{\infty} A(y)dy = \int_{-\infty}^{\infty} e^{-y^2}Qdy = Q\int_{-\infty}^{\infty} e^{-y^2}dy = Q^2