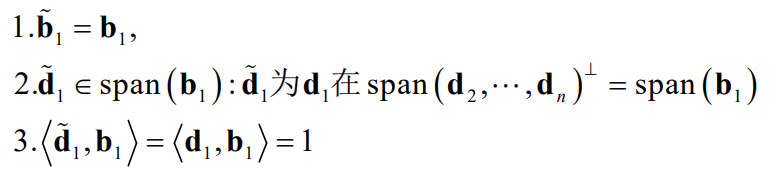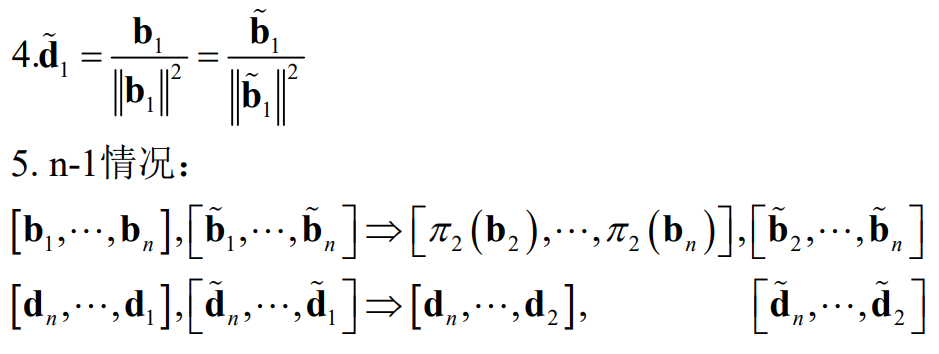格密码基础:对偶格(超全面)
目录
五. 对偶格的转移定理(transference theorem)
推荐先阅读:
一. 对偶格的格点
1.1 基本定义
对偶格(dual lattice)也被称之为倒易格(reciprocal lattice)。原来满秩的格写做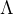 ,其对偶格的定义如下:
,其对偶格的定义如下:
![]()
原来的格点和对偶格的任意(这两个字非常重要)格点相乘为整数即可。原来的格点如果为整数,那么对偶格里有可能会出现小数。此处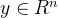 代表n维实数空间,更准确来讲,对偶格应该在原来格的扩展空间内。那么对偶格更准确的定义,如下:
代表n维实数空间,更准确来讲,对偶格应该在原来格的扩展空间内。那么对偶格更准确的定义,如下:
![]()
对偶格的右上角经常带“*”, 代表格的扩展空间。
代表格的扩展空间。
对偶格的重心在于,向量相乘为整数。当然,对偶格也是一种格,格的一些基本性质对偶格也具有。格和对偶格是成对出现的。
1.2 对偶格的例子
整数格的对偶格是其本身,也就是:

也就是整数格满足自对偶的性质。
如果把整数格的格点都扩大两倍,则形成子格。该格的对偶格则会出现小数,如下:
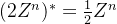
此处的系数有点类似倒数的感觉。
原始格的安全性在对偶格中依旧是存在的。
1.3 对偶格的图形理解
思考:给出任意一个向量点x,请找出所有跟这个向量点乘积为整数的点?
备注:向量与向量相乘为标量
线性代数告诉我们这些点会形成一个超平面,点跟点之间的距离为1/||x||。看一个二维的图形就很直接:
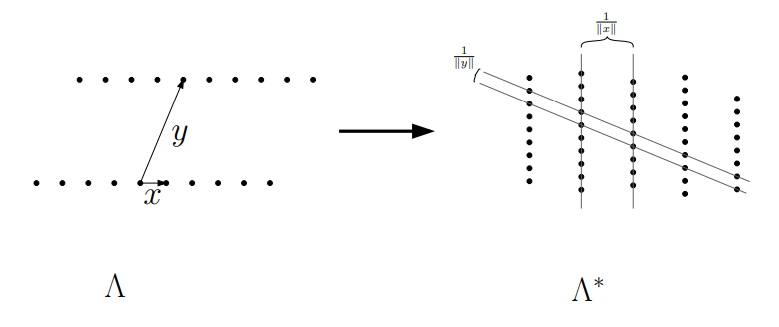
二. 对偶格的格基
格点相乘为整数,那这两个格的格基满足什么性质?
2.1 基本定义
原来的格基叫B,写做:
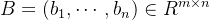
格基内每个向量都是m维,一共有n个向量。
对偶格的格基维度肯定是保持不变的,也就是:

对偶格和原来的格扩展空间肯定一致(向量点维度不一样的话,都不能相乘):

刚才发现对偶格有点倒数的感觉,反应在矩阵上则互逆,所以满足:

单位阵对角线上全为1,其他位置均为0。那么矩阵互逆告诉我们,向量位置一致时,相乘为1,也就是:
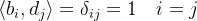
向量位置不一致时,相乘为0:
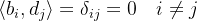
如果格基为方阵,也就是格满秩,则可以直接求逆,那么:
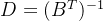
如果格基非方阵,也就是格非满秩,那么可以利用伪逆:
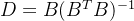
综合以上,对偶格的格基D需要满足两个性质:
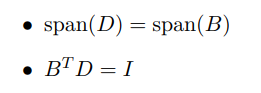
通过以上公式可以发现,只要B确定了,对偶格的格基D也是唯一确定的。
为什么格基满足如上性质,就可以是对偶格?请看2.2
2.2 对偶格的格基证明
本质就是需要证明:

借鉴集合相等的证明思路,我们的证明分成两步。
第一步:证明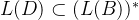
从格L(B)内选取一个格点x,也就是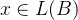 ,将其写做整数倍的向量求和形式:
,将其写做整数倍的向量求和形式:
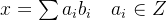
从格基D中随机抽取一个向量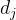 ,运算可得:
,运算可得:
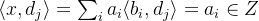
第一个等号:将格点x直接带入;
第二个等号:矩阵B与矩阵D互逆;
因为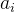 一定为整数,这个时候说明格基D中的每一个列向量都可以算做一个对偶格的格点。格点的求和运算具有封闭性,继续对这些对偶格点进行整数组合也一定是对偶格点,所以可得:
一定为整数,这个时候说明格基D中的每一个列向量都可以算做一个对偶格的格点。格点的求和运算具有封闭性,继续对这些对偶格点进行整数组合也一定是对偶格点,所以可得:
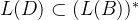
第二步:证明
从对偶格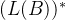 内随机取一个格点y,也就是:
内随机取一个格点y,也就是:
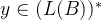
根据对偶格的定义,易得:
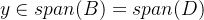
根据扩展空间的定义,那么就可以将该点写做:
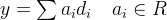
将对偶格的格点和原格的某个格基向量相乘,可得:
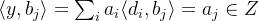
所以可得:
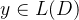
综上第一步和第二步,证明完毕。
三. 对偶格的行列式
对偶格的行列式与原来格的行列式互为倒数,也就是:
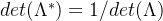
证明:
3.1 满秩格
将格基先转置在求逆,即为对偶格,所以可得:
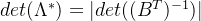
逆矩阵的行列式与原矩阵的行列式互为倒数,所以可得:
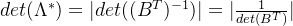
矩阵转置不影响行列式的值,所以可得:
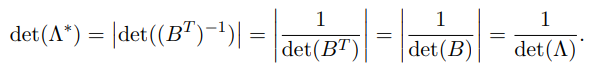
3.2 非满秩格
非满秩格不能直接求逆,则需要借助伪逆,运算性质与以上类似,可得:
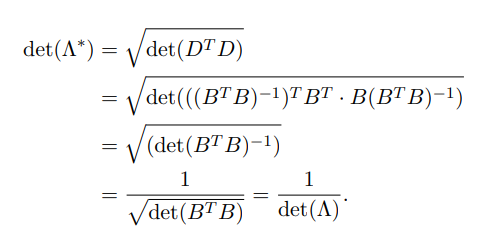
四. 重复对偶格
对偶格的对偶,即为原格,也就是:
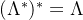
证明:
考虑一般情况。记原格 的格基为B,那么对偶格的格基为:
的格基为B,那么对偶格的格基为:
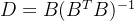
继续对格L(D)求对偶格,也就是运算:
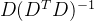
带入运算可得:
![]()
五. 对偶格的转移定理(transference theorem)
本小节需要用到这篇博客的结论:
假定格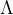 的秩为n,对偶格的最短向量长度满足:
的秩为n,对偶格的最短向量长度满足:
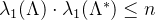
证明:
首先根据闵可夫斯基上界(Minkowski's bound),可得:
![]()
将其类推到对偶格,可得:
![]()
两者相乘可得:
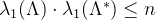
备注:根据Banaszczyk定理,这个界可以继续被放缩,可得:
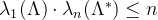
六. 对偶格的连续最小值
本小节需要利用此篇博客的基础知识:
假定格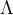 的秩为n,可得:
的秩为n,可得:
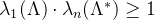
证明:
假定v为原来的格最短的向量点,也就是:
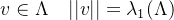
从对偶格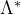 中取n个线性独立的向量:
中取n个线性独立的向量:
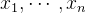
根据格点相乘为整数,可得:
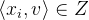
这两个向量的长度乘积必然大于1,也就是:
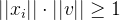
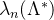 的长度一定比
的长度一定比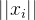 要大,于是乎可得:
要大,于是乎可得:
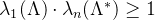
七. 对偶格的正交投影
对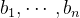 进行Gram-Schmidt正交化,可得:
进行Gram-Schmidt正交化,可得:
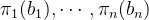
其中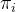 代表将向量投影到前i-1个正交平面上,也就是:
代表将向量投影到前i-1个正交平面上,也就是:

假定B和D互为对偶格基。将矩阵B进行正交投影,可得:
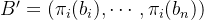
此处就是把向量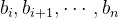 往同一个正交平面进行投影。
往同一个正交平面进行投影。
该格基的对偶格基与原来保持不变,也就是
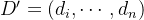
证明:
从扩展平面角度来讲,可得:
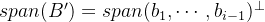
根据对偶格基的性质。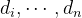 与
与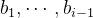 互相垂直,任意向量之间同样两两独立。换句话说,也就是:
互相垂直,任意向量之间同样两两独立。换句话说,也就是:
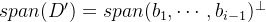
所以可得:
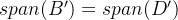
满足对偶格基的第一个性质。
根据向量相乘的性质,不难计算:
![]()
根据逆矩阵的性质,不难证明原定理。
八. 对偶格基的正交化
原格基为:
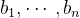
Gram-Schmidt正交化为:
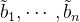
对偶格基:
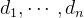
按反方向,Gram-Schmidt正交化为:
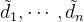
长度满足:
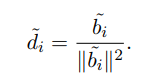
证明:通过以上对偶格基长度讨论易得。也可以用归纳法: