【算法】怎么用算法给外卖小哥规划路线
前言
假设现在外卖小哥接了10个单,那么要怎么规划路线呢?当然,经验丰富的老哥一看就知道了,但是新人菜鸟小哥就未必能找到节省时间的路线。

那么,如果使用算法来解决这个问题会怎么样?如何在尽量少的总路程和时间内,选择一条优秀路线呢?不妨使用搜索算法来解决这个问题,例如遗传算法就可以解决这类型的问题。
主要包括两步
1.A、B两点之间的代价函数
这里的代价不仅是时间,也要考虑路程,难易程度等。当然,只考虑时间也是可以的,主要看小哥自己认为代价是什么。
2.寻找最优路径
使用优化算法,寻找一条总代价最小的路径就可以了。可以使用遗传算法、模拟退火算法、PSO算法等等。
一、送餐的代价函数
我们需要考虑到多种因素,包括但不限于:
1.交通状况:交通状况是影响外卖小哥送餐速度的重要因素之一。规划路线时需要考虑到交通拥堵、红绿灯等因素,选择最佳的路线。
2.餐厅出餐速度:外卖小哥需要考虑到餐厅出餐速度,避免等待时间过长,影响送餐速度。
3.客户要求:有些客户可能有特殊要求,比如需要外卖小哥爬楼梯等,规划路线时需要考虑到这些因素
对上述每个因素,都分别进度量,最后综合,从而得到两点之间的代价函数C(A,B).
二、送餐的最优路径
接下来,就是一个TSP的问题了,也就是求解如何走完所有取餐、送餐点,并使得总代价时间最小。在这里,我们不妨使用遗传算法,
2.1 遗传算法简介
遗传算法(Genetic Algorithm,GA)是由美国的John Holland教授于20世纪70年代首次提出的,它是一种自适应随机搜索启发式算法。遗传算法以自然选择规律与遗传理论为依托,模拟生物进化过程中的遗传、交叉、变异等过程,通过数学的方式利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。
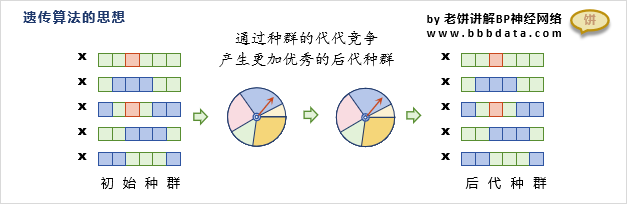
遗传算法在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。它被广泛应用于复杂函数系统优化、机器学习、系统识别、故障诊断、分类系统、控制器设计、神经网络设计、自适应滤波器设计等领域。
详细可参考《老饼讲解|【原理】遗传算法-入门讲解》
2.2 遗传算法的算法流程
遗传算法的算法流程如下
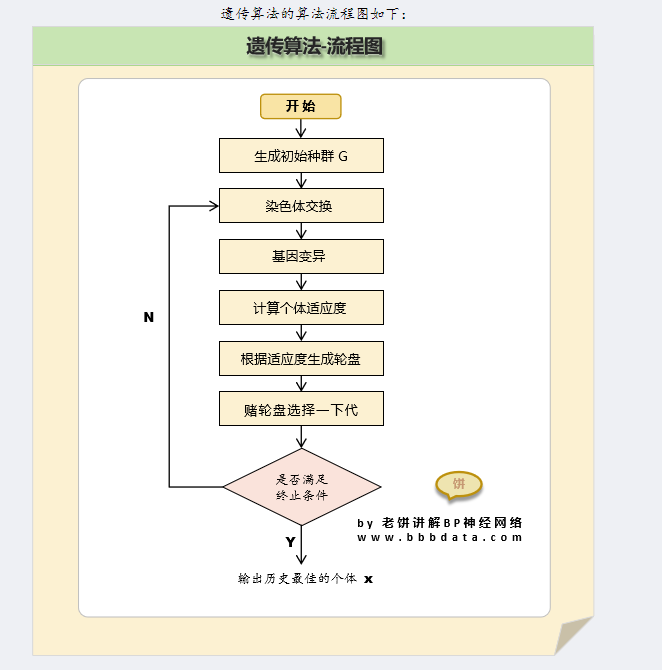
2.3 遗传算法应用于路径规划
用遗传算法,需要设计好该问题的以下三点:
👉1. 染色体交换方式:解与解之间如何进行部分交换
👉2. 基因变异的方式:单个解如何作出随机改变
👉3. 适应度的定义 :用于评估解的优秀程度
对本问题我们可以设计如下:
(1)遗传算法染色体交换方式
将解群两两随机配对,每一对之间(设为a,b)以如下方式交换:
设a=[0,1,5,3,2,4],b=[1,2,5,0,3,4],先随机抽出a的一个片段a_piece,
假设a_piece= [5,3,2],再在b中找出 a_piece 的排序 b_piece=[2,5,3],
将b_piece替换到a,将a_piece替换到b,得到:a=[0,1,2,5,3,4],b=[1,5,3,0,2,4]
(2)遗传算法基因变异方式
设a=[0,1,5,3,2,4],
先随机抽出a的一个片段a_piece,假设a_piece= [5,3,2],
将a_piece翻转( [2,3,5])后再回代a,得到a=[0,1,2,3,5,4]
(3)遗传算法适应度设计:
本问题的目标函数一定是大于0的,我们简单的设为 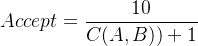
即可(F是目标函数的值),就可以达到函数值越小,适应度越大的效果。
设计完以上三点后,只需按遗传算法的算法流程,实现代码即可
三、送餐的最优路径-代码实现
3.1代码说明
下面,我们使用代码实现上述算法。但为了便于实现,作出如下两点假设与简化:
1.由于我们还没有得到任意两点A、B之间的代价函数C(A,B)的具体表达式,而为了能够实现代码,我们不妨先用距离函数D(A,B)替代代价函数C(A,B),
2.对于地点之间的路线和交通是复杂的,需要依赖了第三方服务的支持,这里我们简单为两点的直线距离就好,
3.2 遗传算法规划路径-代码实现
代码实现如下:
%------代码说明:展示遗传算法求解TSP问题 -----------------
% 来自《老饼讲解神经网络》www.bbbdata.com ,matlab版本:2018a
function gaforTSP()
clc;clear all;close all ;
rng(999)
global distMat;
cityLoc = [3.64,2.68 ;...
4.18,1.76 ;...
3.71,2.60 ;...
1.33,3.30 ;...
4.20,2.96 ;...
3.92,1.82 ;...
2.55,1.64 ;...
2.37,1.02 ;...
3.43,2.09 ;...
3.54,0.70 ;...
3.51,1.62 ;...
3.44,0.80 ;...
3.24,2.77 ;...
2.38,2.32 ;...
2.56,2.24 ;...
3.01,2.03 ;...
2.79,2.51 ;...
4.03,1.16 ;...
3.47,0.70 ;...
1.30,1.69] ;
distMat = dist(cityLoc') ; % 计算城市距离
N = size(cityLoc,1); % 城市个数
rng(888) % 为方便复现结果,设定随机种子
%----------------参数初始化-----------------------
m = 30; %种群规模
t = 5000; %迭代次数
var_rate = 0.2; %变异概率
%--------------初始化种群-------------------------
xg = cell(m,1); % 初始化种群
for i =1:m
xg{i} = randperm(N); % 随机初始化种群
end
h_best_x = xg{1}; % 初始化历史最优个体
h_best_F = calF(h_best_x); % 初始化历史最优个体的目标函数值
F_list = []; % 每代最优函数值记录列表
for i=1:t
% ----种群交换染色体与基因变异-----
xg = exPart(xg); % 交换染色体
xg = genVar(xg,var_rate); % 基因变异
[best_x,best_F] = getBest(xg); % 获取本代最佳个体
if(best_F <h_best_F) % 更新历史最优个体
h_best_F = best_F; % 更新历史最优函数值
h_best_x = best_x; % 更新历史最优个体
end
disp(['第',num2str(i),'代:最优F=',num2str(best_F)]) % 显示当前轮的最优个体
F_list = [F_list,best_F]; % 记录历代最优个体
% 判断是否满足退出迭代条件.
% 退出条件:近20代最优个体变化不大,则退出
last_F = F_list(max(1,end-20):end); % 截取最后20轮的最佳函数值
diff = (max(last_F)-min(last_F))/max(abs(mean(last_F)),1); % 最近20轮的差异
if((i>20) && (diff<0.001)) % 判断没什么差异
break % 则退出迭代
end
%-------------赌轮盘生成下一代---------------------------
PPan = getPPan(xg); % 计算种群的概率轮盘
xg = genChildGroup(xg,PPan,h_best_x); % 根据概率轮盘选出下一代种群
%------------------画图------------------------------------
hold off
plot(cityLoc(:,1),cityLoc(:,2),'o','MarkerEdgeColor','k','MarkerFaceColor','y','MarkerSize',10,'LineWidth',2)
hold on
plot(cityLoc([h_best_x,h_best_x(1)],1),cityLoc([h_best_x,h_best_x(1)],2))
drawnow
end
% 打印最终结果(历史最优)
disp(['h_best_F=',num2str(h_best_F)]) % 打印历史最优目标函数值
disp(['h_best_x=',num2str(h_best_x)]) % 打印历史最优个体
end
%------------目标函数值计算方法------------------------------------------
function d= calF(x)
global distMat;
d = distMat(x(end),x(1)); % 初始化总距离
for i=1:length(x)-1
d = d+ distMat(x(i),x(i+1)); % 累加各个城市之间的距离
end
end
%------------获取种群中目标函数值最好的一个-------------------------------
function [x,F] = getBest(xg)
F_list = inf(length(xg),1); % 初始化各个个体的函数值
for i = 1:length(xg)
F_list(i) = calF(xg{i}); % 计算各个个体的目标函数值
end
[F,best_index] =min(F_list) ; % 获取最优的目标函数值与索引
x = xg{best_index}; % 根据索引获取最优的个体
end
%------------计算种群进入下一代的概率轮盘-----------------
function PPan = getPPan(xg)
F_list = inf(length(xg),1); % 初始化各个个体的函数值
for i = 1:length(xg)
F_list(i) = calF(xg{i}); % 计算各个个体的目标函数值
end
F_list = F_list - min(F_list); % 令函数值全大于0
acp_list = 1./(1+F_list); % 计算适应度
PPan = cumsum(acp_list./sum(acp_list)); % 根据适应度计算轮盘概率
end
%------------染色体交换-------------------------------
function xg = exPart(xg)
m = length(xg); % 种群大小
[vn,n] = size(xg{1}); % 变量个数,编码长度
ex_list = randperm(m); % 随机生成种群排序,用于下面两两匹对交换
for i=1:2:m % 逐对交换
a = xg{ex_list(i)}; % 当前要交换的个体a
b = xg{ex_list(i+1)}; % 当前要交换的个体b
ex_part = randperm(n); % 随机生成1到n的随机整数
ex_part = ex_part(1:2); % 提取前两位作为要交换的起始结束位置
ex_start = min(ex_part); % 小者作为交换的起始位置
ex_end = max(ex_part); % 大者作为交换的结束位置
a_piece = a(ex_start:ex_end); % 提出出a要交换的片段
[~,idx] = ismember(a_piece,b); % 找出a的片段在b中的位置
idx = sort(idx); % 对位置进行排序
b_piece = b(idx); % 提出b中的片段
a(ex_start:ex_end) = b_piece; % 将b的片段赋予a
b(idx) = a_piece; % 将a的片段赋予b
xg{ex_list(i)} = a; % 将个体a重新替换回种群
xg{ex_list(i+1)} = b; % 将个体b重新替换回种群
end
end
%------------基因变异-------------------------------
function xg = genVar(xg,var_rate)
m = length(xg); % 种群大小
[~,n] = size(xg{1}); % 编码长度
for i= 1:m
a = xg{i}; % 提取出当前个体
if(rand()<var_rate) % 判断当前个体是否变异
var_part = randperm(n); % 随机生成变异的位置
var_part = var_part(1:2); % 截断前两位作为变异起始结束位置
var_start = min(var_part); % 小者作为变异起始位置
var_end = max(var_part); % 大者作为变异结束位置
a(var_start:var_end) = flip(a(var_start:var_end)); % 将变异位置翻转
end
xg{i} = a ; % 将变异后的个体替换进种群
end
end
%------------生成下代种群-------------------------------
function child_xg = genChildGroup(xg,PPan,best_x)
m = length(xg); % 种群个数
child_xg = cell(m,1); % 初始化下一代种群
child_xg{1} = best_x; % 最佳的必定选到下一个种群
for i=2:m
select_idx = min(find(rand()<PPan)); % 生成一个随机数,并找到第一个小于该随机数的位置,就是轮盘指向的位置
child_xg{i} = xg{select_idx}; % 将轮盘选出的个体选入下一代种群
end
end运行后的结果如下:
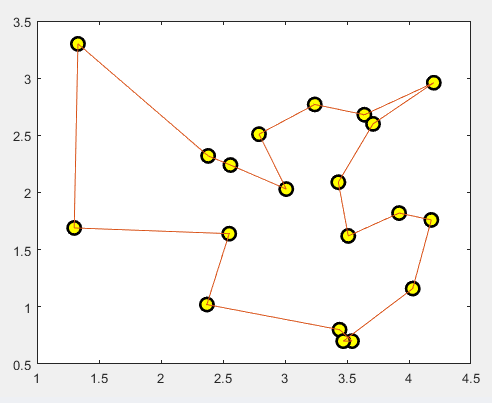
如果觉得本文有帮助,点个赞吧!