机器学习分类算法_机器学习分类算法(一)逻辑回归

逻辑回归算法原理推导

• 逻辑回归属于分类算法，做的是分类任务，是一种经典的二分类算法！
• 因为应用的比较广泛，且表现效果不错。如果做的是分类任务，可以先考虑逻辑回归。
• 也可以使用逻辑回归解决多分类问题(softmax)
• 机器学习算法选择：先逻辑回归再用复杂的，能简单还是用简单的。越复杂的结构内部解释起来越复杂，越简单的结构内部解释起来越简单。
• 逻辑回归的决策边界：可以是非线性的

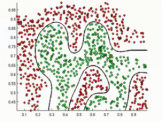
Sigmiod函数

• 公式：
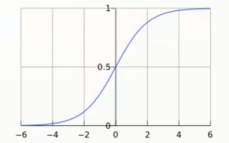
• 自变量取值为任意数，值域[0,1]
• 解释：将任意的输入映射到了[0,1]区间。我们在线性回归中可以得到一个预测值，再将该值映射到SIgmoid函数中，这样就完成了由值到概率的转换，如果结果大于50%可以设定为0，如果小于50%可以设定为1，也就是分类任务。
• 预测函数：其中，， 输入是,有多少个特征就有多少个输入。
• 分类任务：，整合一下就是
• 解释，对于二分类任务(0,1),整合后y取0只保留，y取1只保留

逻辑回归求解

• 似然函数：
• 对数似然：
• 此时应用梯度上升求最大值，引入转换为梯度下降任务，求正数的最大值，也就是求负数的最小值。
• 求导过程。计算每个参数梯度方向，计算出偏导数。求解什么样的方式是最合适的，有多少个就对多少个求偏导

其中表示第几个样本,表示第几个特征 1/m表示综合考虑所有样本 *多分类的softmax

逻辑回归手写算法实现

我们先来简单看个例子，使用逻辑回归预测学生能否被录取。我们将建立一个逻辑回归模型来预测一个学生是否被大学录取。假设你是一个大学的管理员你想根据两次考试的结果来决定每个申请人的录取机会。你有以前的申请人的历史数据，你可以根据它作为逻辑回归的训练集。对于每一个培训例子，你有两个考试的申请人的分数和录取决定。为了做到这一点，我们将建立一个分类模型，根据考试成绩估计入学概率。

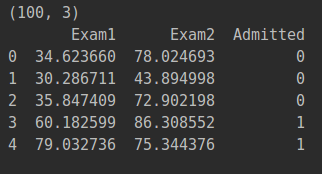
1.读取数据

pdData=pd.read_csv('LogiReg_data.txt',header=None,names=['Exam1','Exam2','Admitted']);
print(pdData.shape)
print(pdData.head())

2.将数据集中的正类(1:同意入学)和负类(0:拒绝入学)可视化

positive=pdData[pdData['Admitted']==1]
negative=pdData[pdData['Admitted']==0]

fig,ax=plt.subplots(figsize=(10,5))#指定画图域的大小
ax.scatter(positive['Exam1'],positive['Exam2'],s=30,c='b',marker='o',label='Admitted')
ax.scatter(negative['Exam1'],negative['Exam2'],s=30,c='r',marker='x',label='Not Admitted')
ax.legend()
ax.set_xlabel("Examl Score")
ax.set_xlabel('Exam2 Score')
plt.show()

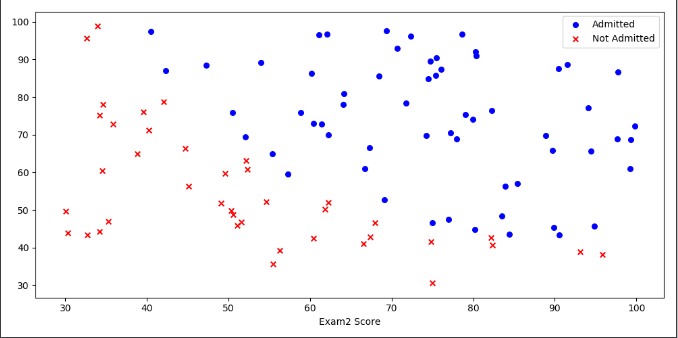其中，横坐标是Exam1，纵坐标是Exam2，通过和不通过的数据颜色分别设置成蓝色和红色，用圆圈和叉号表示数据分布，标签设置成Admitted和Not Admitted.

从图中可以很容易看出啊，有一条决策边界可以将数据完美分开。

我们接下来就是用上面所说的案例和数据，手写逻辑回归算法。

梯度下降求解逻辑回归

目标：建立分类器，求解出三个参数，，，其中，代表两列考试成绩的参数，代表偏置项的参数。

设定阈值，根据阈值判断录取结果，阈值我们一般取0.5，大于0.5表示被录取，小于0.5表示没有被录取。

要完成的模块：

• sigmoid：映射到概率的函数
• model：返回预测结果值
• cost：根据参数计算损失值
• gradient：计算每个参数的梯度方向
• descent：进行参数更新
• accuracy：计算精度

sigmoid：映射到概率的函数

def sigmoid(z):
    return 1/(1+np.exp(-z))

参数z是线性回归传过来的值，通过sigmoid函数，将数值转换为0-1之间的概率值。

为了对sigmoid函数有更好的理解，我们可视化这个函数。

nums=np.arange(-10,10,step=1)
fig,ax=plt.subplots(figsize=(10,4))
ax.plot(nums,sigmoid(nums),'r')
plt.show()

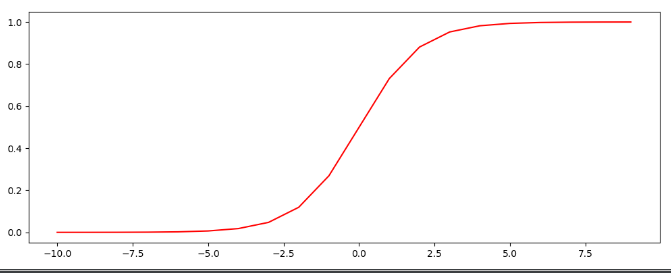横坐标是-10~10之间的数字，步长是1。

model：返回预测结果值

def model(X,theta):
    return sigmoid(np.dot(X,theta.T))

在这里，我们需要两个参数X和,预测结果的公式可以这样表示

这里的，，分别表示偏置项参数、第一个成绩的参数、第二个成绩的参数。，，分别代表偏置项、第一个成绩和第二个成绩。

也就是预测函数：

我们首先获取包含偏置项的X数据和预先定义的theta参数：

pdData.insert(0,'ones',1) #数据中插入一列都是1，列名是ones

orig_data=pdData.as_matrix() #将数据转换成数组
cols=orig_data.shape[1] #查看数组列数
X=orig_data[:,0:cols-1]
y=orig_data[:,cols-1:cols]
theta=np.zeros([1,3])

本来是3列，现在变成4列：偏置项、两列成绩和标签。

我们看一下新生成的数据格式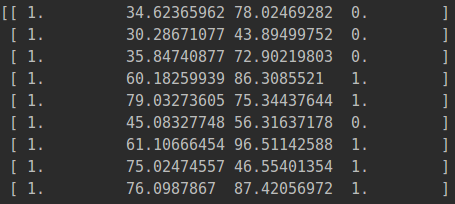：我们再将数据带入到model函数中，对结果进行预测。由于我们定义的theta参数都为0，所以sigmoid函数在theta没有更新之前肯定每个结果都是1/(1+1))=0.5

def model(X,theta):
    return sigmoid(np.dot(X,theta.T))

result=model(X,theta)
print(result)

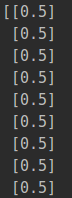
cost：根据参数计算损失值

我们上面说过，似然公式为：

对数似然公式为：

我们要求其最大值，所以引入转换为梯度下降任务，求其最小值。

所以现在公式变为：

求平均损失：

def cost(X,y,theta):
    left=np.multiply(-y,np.log(model(X,theta)))
    right=np.multiply(1-y,np.log(1-model(X,theta)))
    return np.sum(left-right)/len(X)

print(cost(X,y,theta))

完全按照公式写入，得出平均损失函数。

gradient：计算每个参数的梯度方向

我们把上面之前推导的公式再看一遍：

有多少个参数就计算多少个梯度

def gradient(X,y,theta):
    grad=np.zeros(theta.shape) #有多少个参数就有多少个梯度
    error=(model(X,theta)-y).ravel() #将多维函数转换为1维函数
    for j in range(len(theta.ravel())):
        term=np.multiply(error,X[:,j]) #取第j列的所有样本
        grad[0,j]=np.sum(term)/len(X)
    return grad


print(gradient(X,y,theta))

每个参数的梯度方向，通过偏导数得出。

descent:进行参数更新

下面我们将通过实验比较三种不同梯度下降算法。

之前我们在线性回归讲过三种不同梯度下降函数，分别是批量梯度下降(全部样本)、随机梯度下降(随机选择一个)和小批量梯度下降(随机选择一部分样本)，我们将测试哪种更好。

先将数据原有的顺序打乱，这样使得模型的泛化能力更强。

def shuffleData(data):
    np.random.shuffle(data)
    cols=data.shape[1]
    X=data[:,0:cols-1]
    y=data[:,cols-1:cols]
    return X,y
    
print(shuffleData(orig_data))

descent:进行参数更新，分别计算出参数、迭代次数、损失值、梯度值、消耗时间

STOP_ITER = 0  # 迭代次数
STOP_COST = 1  # 损失值
STOP_GRAD = 2  # 梯度

def stopCriterion(type,value,threshold):
    if type==STOP_ITER:
        return value>threshold
    elif type==STOP_COST:
        return abs(value[-1]-value[-2]    elif type==STOP_GRAD:
        return np.linalg.norm(value)
def descent(data, theta, batchSize, stopType, thresh, alpha):
    # 梯度下降求解
    init_time = time.time()
    i = 0  # 迭代次数
    k = 0  # batch
    X, y = shuffleData(data)
    grad = np.zeros(theta.shape)  # 计算的梯度
    costs = [cost(X, y, theta)]  # 损失值

    while True:
        grad = gradient(X[k:k + batchSize], y[k:k + batchSize], theta)
        k += batchSize  # 取batch数量个数据
        if k >= n:
            k = 0
            X, y = shuffleData(data)  # 重新洗牌
        theta = theta - alpha * grad  # 参数更新
        costs.append(cost(X, y, theta))  # 计算新的损失
        i += 1

        if stopType == STOP_ITER:
            value = i
        elif stopType == STOP_COST:
            value = costs
        elif stopType == STOP_GRAD:
            value = grad
        if stopCriterion(stopType, value, thresh):
            break

    print("参数值:",theta)
    print("迭代次数:",i-1)
    print('损失值',costs)
    print("梯度:",grad)
    print("消耗时间",time.time() - init_time)

首先介绍下其中的参数：

• data：数据集
• theta：参数
• batchsie：表示参与的样本个数
• stopType:表示停止策略
• thresh：表示策略对应的阈值
• alpha:表示学习率

在算法中我们有个疑问，那就是到底迭代多少次才合适呢？这里我们有三个方法来判断停止。

• 通过迭代次数。假设设置阈值为5000，表明迭代5000次则结束
• 通过损失值，达到我们给出的损失值就停止
• 通过给出梯度值，达到这个梯度那么就停止

我们首先根据迭代次数进行停止

n=100#全部样本参与测试

descent(orig_data, theta, n, 0, thresh=5000, alpha=0.000001)

我们利用图形可视化参数

def runExpe(data, theta, batchSize, stopType, thresh, alpha):

    theta, iter, costs, grad, dur = descent(data, theta, batchSize, stopType, thresh, alpha)

    name = "Original" if (data[:,1]>2).sum() > 1 else "Scaled"
    name += " data - learning rate: {} - ".format(alpha)
    if batchSize==n:
        strDescType = "Gradient"
    elif batchSize==1:
        strDescType = "Stochastic"
    else:
        strDescType = "Mini-batch ({})".format(batchSize)
    name += strDescType + " descent - Stop: "
    if stopType == STOP_ITER:
        strStop = "{} iterations".format(thresh)
    elif stopType == STOP_COST:
        strStop = "costs change .format(thresh)else:
        strStop = "gradient norm .format(thresh)
    name += strStopprint ("***{}\nTheta: {} - Iter: {} - Last cost: {:03.2f} - Duration: {:03.2f}s".format(
        name, theta, iter, costs[-1], dur))
    fig, ax = plt.subplots(figsize=(12,4))
    ax.plot(np.arange(len(costs)), costs, 'r')
    ax.set_xlabel('Iterations')
    ax.set_ylabel('Cost')
    ax.set_title(name.upper() + ' - Error vs. Iteration')
    plt.show()

1.如果我们选择的样本是全部数据参与，停止策略是根据迭代次数停止。

#选择的梯度下降方法是基于所有样本的
n=100
#根据迭代次数停止
runExpe(orig_data, theta, n, STOP_ITER, thresh=5000, alpha=0.000001)

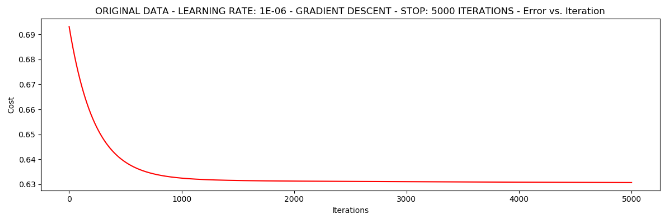可以看出迭代5000次后，损失值趋向于不变。但是不要被结果所迷惑，说不定损失值还是会变化，通常要多做一些尝试。

2.如果我们选择的样本是全部数据参与，停止策略是根据损失值。

runExpe(orig_data, theta, n, STOP_COST, thresh=0.000001, alpha=0.001)

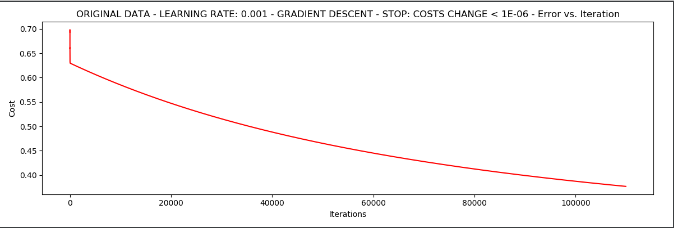可以看出消耗的时间更长，且需要迭代大概110000次，阈值我们设定为0.000001.

3.如果我们选择的样本是去全部数据参与，停止策略是根据梯度值。

设定阈值为0.05，差不多需要40000次迭代

runExpe(orig_data, theta, n, STOP_GRAD, thresh=0.05, alpha=0.001)

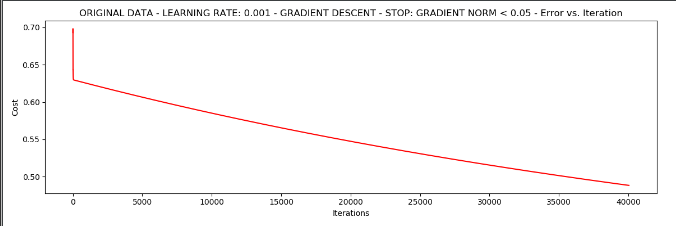4.我们使用样本是1个，停止策略是迭代次数。

runExpe(orig_data, theta, 1, STOP_ITER, thresh=5000, alpha=0.001)

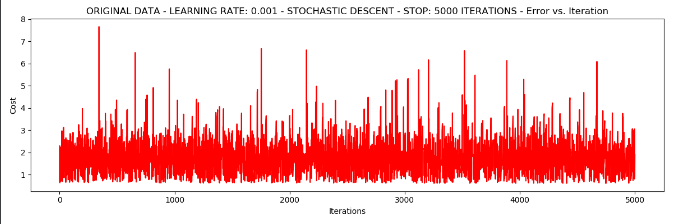这样效果并不好，损失值很高，不收敛。

5.我们尝试把学习率降低，看效果会不会好

runExpe(orig_data, theta, 1, STOP_ITER, thresh=15000, alpha=0.000002)

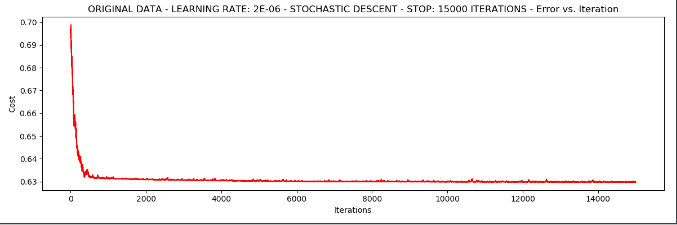我们发现把学习率调小，损失值可以接近收敛，但不是特别好。总而言之就是速度快，稳定性差。

6.我们随机选取16个样本，停止策略是迭代次数

runExpe(orig_data, theta, 16, STOP_ITER, thresh=15000, alpha=0.001)

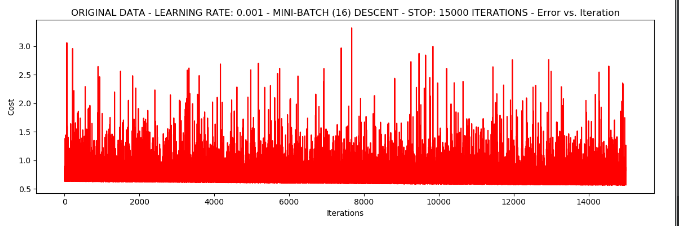发现浮动仍然比较大。

我们来尝试下对数据进行标准化，将数据按其属性(按列进行)减去均值，然后除以方差。最后的到的结果是，对每个属性/每列来说所有数据都聚集在0附近，方差值为1.

from sklearn import preprocessing as pp
scaled_data = orig_data.copy()
scaled_data[:, 1:3] = pp.scale(orig_data[:, 1:3])
runExpe(scaled_data, theta, n, STOP_ITER, thresh=5000, alpha=0.001)

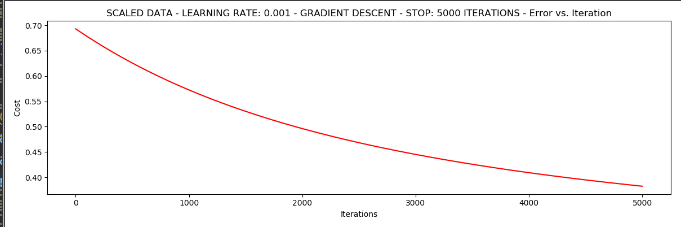从图中可以看出，原始数据的损失值最高只能达到0.61，而现在达到了0.38.所以对数据做预处理是非常重要的。

# 我们停止策略采用梯度值
from sklearn import preprocessing as pp
scaled_data = orig_data.copy()
scaled_data[:, 1:3] = pp.scale(orig_data[:, 1:3])
runExpe(scaled_data, theta, n, STOP_GRAD, thresh=0.02, alpha=0.001)

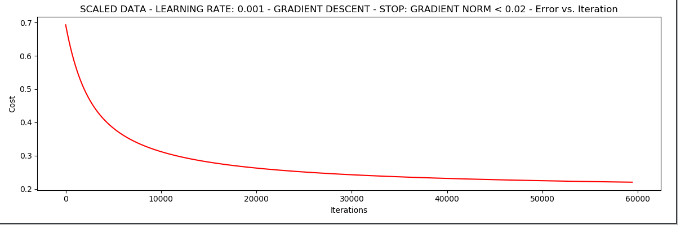发现我们给出了固定的损伤值，那么迭代次数60000次才达到这个效果。

#样本采用16个值，停止策略是梯度值。
runExpe(scaled_data, theta, 16, STOP_GRAD, thresh=0.002*2, alpha=0.001)

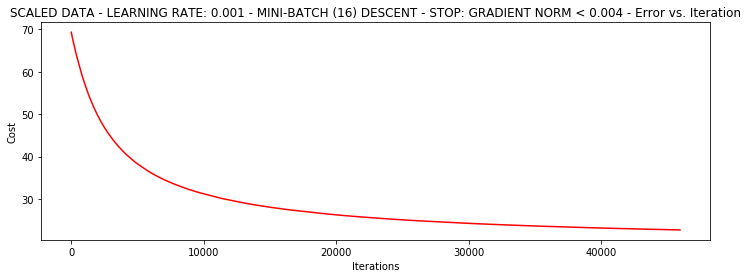
accuracy:计算精度

def predict(X,theta):
    return [1 if x>= 0.5 else 0 for x in model(X,theta)]

scaled_x=scaled_data[:,:3]
y=scaled_data[:,3]

predictions=predict(scaled_x,theta)

correct=[1 if((a==1 and b==1) or (a==0 and b==0)) else 0 for (a,b) in zip(predictions,y)]
accuracy=(sum(map(int,correct)) % len(correct))
print('accuracy={0}%'.format(accuracy))

最终计算出，accuracy = 60%

案例-交易数据异常检测

之前学习了逻辑回归的原理和算法，那么我们该如何应用呢？

先看一下数据：

data=pd.read_csv('creditcard.csv')
print(data.head())

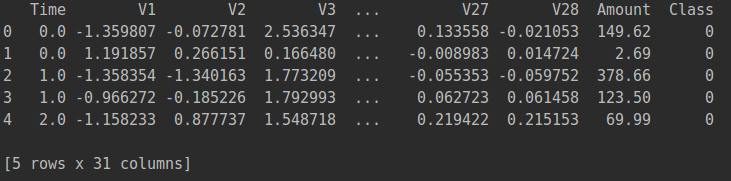可以看出数据的特征比较多。简单看一下特征：

• time这一列表示交易持续的时间,在这里没多大的意义。.
• v1,v2,v3.....v28分别代表特征1,2,3.....28.考虑到用户的隐私,对部分数据进行了处理。
• Amount代表交易的金额,这个金额相比特征的数据浮动比较大,因此会对Amount这一列的数据进行预处理.
• Class 中代表是正常样本,1代表异常样本

这个案例的目的是做信用卡的欺诈检测.在欺诈数据里面,有正常的数据,也有不正常的数据.因此对于这样的问题,我们可以将原始问题分为0类是正常的、1类是异常的,接下来就是对样本的数据进行0和1的分类,相当于二分类的问题.

用这些已经提取好的特征,如何进行建模的操作呢?接下来用逻辑回归,建立一个模型.

首先看一下样本数据的分布规则,一般情况下正常数据出现的情况比较多,异常数据出现的情况比较少.一般99.9%的数据都是正常的,只有那么0.1%的数据出现诈骗或者异常或者其他.因此这个样本数据的检测绝大多数都是正常样本,只有极少数的样本是异常样本.

首先看一下正负样本的比例有多大？

data=pd.read_csv('creditcard.csv')

count_classes=pd.value_counts(data['Class'],sort=True).sort_index()

count_classes.plot(kind='bar') #条形图
plt.title('Fraud class histogram')
plt.xlabel('Class')
plt.ylabel('Frequency')
plt.show()

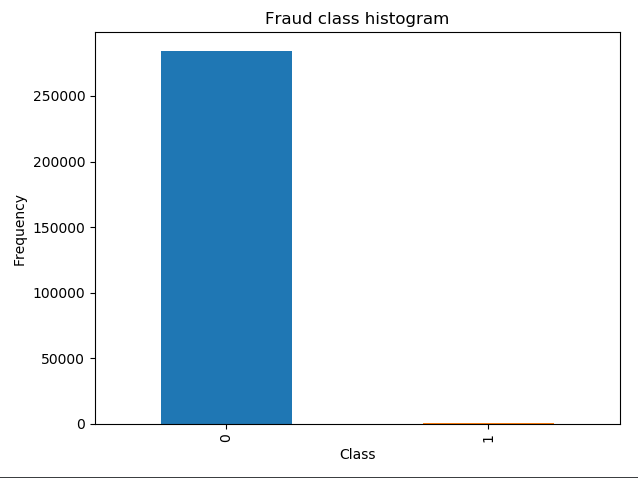丛输出的结果可以看出样本数据的差异，正常的样本0有84315个，异常的样本1非常少，只有492个。

样本不均衡解决方案

这里需要想一下,我们如何解决样本数据不均衡这种情况?像题目中给出的样本数据是极度不均衡的(正样本数量太多),应该如何解决?

这里有两种解决方案,一是过采样,一种是下采样,这是针对样本不均衡最常使用的两种方案.

那么什么是下采样呢？

就是当数据样本不均衡,想变成均衡的数据,将0和1的数据一样小.之前统计的结果可以看出0的样本有28万个,而1的样本只有几百个.现在将0的数据也变成几百个就可以了.下采样,是使样本的数据同样少.

过采样定义:之前统计的结果可以看出0的样本有28万个,而1的样本只有几百个.0比较多1比较少,对1的样本数据进行生成数列,让生成的数据与0的样本数据一样多.

这两种方案,那种方案稍微的更好一些呢?

之前有提到Amount 这列的数值浮动比较大,有些值比较小,有些值比较大.在建机器模型的时候,首先要做一件事情,首先要保证特征分布的差异是差不多的,比如拿v28与Amount 来举例.v28的数据分布的区间是[-1,1],Amount 分布差异比较大.

机器学习算法可能有这样的误导,数值比较大的特征那么它的重要程度是偏大一些的;数值比较小的特征,它的重要程度是偏小一些的.因此需要使数据的特征是相当的,避免机器学习算法有误区.

这里并非要求V28与Amount的特征谁更重要一些,因此要对Amount的数据进行规划，要么做标准化.可以将Amount的数据做成区间是[0,1]或者[-1,1],这些都是可以的.在sklearn库中有提供好的预处理模块,可以对数据进行预处理操作.

from sklearn.preprocessing import StandardScaler
data['normAmount']=StandardScaler().fit_transform(data['Amount'].values.reshape(-1,1))
data=data.drop(['Time','Amount'],axis=1) #删除不要的特征
print(data.head())

其中StandardScaler()是标准化的模块，fit_trainsform是对数据进行变化

下采样策略

接下来就是用下采样以及过采样的两种方式,是样本数据进行均衡处理.首先先用下采样的的策略:使0和1的样本数据一样的少,要使0和1的数据一样的少,那么应该怎么做呢?

先对数据进行划分：

X=data.ix[:,data.columns!='Class']
y=data.ix[:,data.columns=='Class']

接下来是让0和1一样的少.因为两者的样本数量超级不均衡,因此需要了解1类的样本数量有多少个?

需要计算Class == 1的样本个数

number_records_fraud=len(data[data.Class==1])
fraud_indices=np.array(data[data.Class==1].index) #将Class=1的样本的索引拿出来

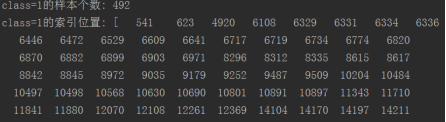可以看出异常样本只有492个。

接下来需要将0类的数据进行随机选择,因此先将将Class = 0的样本的索引拿出来,通过这些索引进行随机的选择.

normal_indices=data[data.Class==0].index

将Class=0的样本的索引进行随机的选择.

np.random.choice(normal_indices, number_records_fraud, replace = False)

对数据进行随机的选择,第1个参数是指待选择的数据,而第2个参数是指选择的个数,第3个参数是否选择代替,这里选择不代替.

random_normal_indices = np.random.choice(normal_indices, number_records_fraud, replace=False)
random_normal_indices = np.array(random_normal_indices)
print("随机选择492个正样本索引输出:",random_normal_indices)

接下来,对numpy的数据进行一个合并的操作.这里的数据index的值是等于1,还有index的值是等于0,将这两组数据放在在一起

under_sample_indices=np.concatenate([fraud_indices,random_normal_indices])
print("class=1和class=0的索引位置合并:",under_sample_indices)

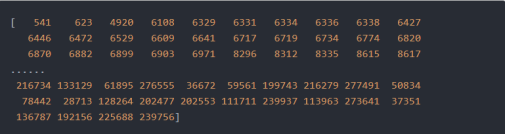
under_sample_data是经过完下采样处理之后,可以再将under_sample_data数据分为2部分的数据,一部分是X_undersample数据,一部分是y_undersample数据,分别是代表是特征以及标签.

under_sample_data = data.iloc[under_sample_indices,:]
#print("下采样之后的数据集:\n",under_sample_data)
X_undersample = under_sample_data.ix[:, under_sample_data.columns != 'Class']
#print("下采样数据集的特征:\n",X_undersample)
y_undersample = under_sample_data.ix[:, under_sample_data.columns == 'Class']
#print("下采样数据集的标签:\n",y_undersample)

打印这样的函数,从输出的结果可以看出下采样的数据共984个,正样本有50%,负样本有50%.通过下采样的方式将0和1不均衡的数据转换成均衡的数据.只是发生了一些代价,产生代价的原因是因为数据是随机生成的,有些数据并非利用到手。

print("Percentage of normal transactions: ", len(under_sample_data[under_sample_data.Class == 0])/len(under_sample_data))
print("Percentage of fraud transactions: ", len(under_sample_data[under_sample_data.Class == 1])/len(under_sample_data))
print("Total number of transactions in resampled data: ", len(under_sample_data))

输出结果为：完整代码如下：

import numpy as np
from sklearn.preprocessing import StandardScaler
import pandas as pd 

data=pd.read_csv("creditcard.csv")
data['normAmount'] = StandardScaler().fit_transform(data['Amount'].reshape(-1, 1))
data = data.drop(['Time','Amount'],axis=1)

X = data.ix[:, data.columns != 'Class']
y = data.ix[:, data.columns == 'Class']
number_records_fraud = len(data[data.Class == 1])
fraud_indices = np.array(data[data.Class == 1].index)
normal_indices = data[data.Class == 0].index
random_normal_indices = np.random.choice(normal_indices, number_records_fraud, replace = False)
random_normal_indices = np.array(random_normal_indices)
print(random_normal_indices)
under_sample_indices = np.concatenate([fraud_indices,random_normal_indices])
under_sample_data = data.iloc[under_sample_indices,:]

X_undersample = under_sample_data.ix[:, under_sample_data.columns != 'Class']
y_undersample = under_sample_data.ix[:, under_sample_data.columns == 'Class']
print("Percentage of normal transactions: ", len(under_sample_data[under_sample_data.Class == 0])/len(under_sample_data))
print("Percentage of fraud transactions: ", len(under_sample_data[under_sample_data.Class == 1])/len(under_sample_data))
print("Total number of transactions in resampled data: ", len(under_sample_data))

我们再思考一下，下采样的操作是否会存在潜在的问题呢？数据量拿出来比较少，肯定会存在一些问题，这个我们会在会面进行讨论。

交叉验证

我们接下来了解下交叉验证.

什么是交叉验证法？

在建立分类模型时，交叉验证(Cross Validation)简称为CV，CV是用来验证分类器的性能。它的主体思想是将原始数据进行分组，一部分作为训练集，一部分作为验证集。利用训练集训练出模型，利用验证集来测试模型，以评估分类模型的性能。

训练数据上的误差叫做训练误差，它对算法模型的评价过于乐观。利用测试数据测量的是测试误差，我门报告的是测试误差。有的时候训练集上的正确率可能达到100%，但是在测试集上可能和随机猜测差不多。

为什么用交叉验证法？

交叉验证用于评估模型的预测性能，尤其是训练好的模型在新数据上的表现，可以在一定程度上减小过拟合。

还可以从有限的数据中获取尽可能多的有效信息。

交叉验证常用的几种方法：

1.去一法  Leave-One-Out Cross Validation(记为LOO-CV)

它的做法是，从训练集中拿出一个样本，并在缺少这个样本的数据上训练出一个模型，然后看模型是否能对这个样本正确分类。假设样本个数有N个，则该方法一共要训练出N个模型，利用这N个模型最终的验证集的分类准确率的平均数作为此下LOO-CV分类器的性能指标。然而随着数据量的增大，工作量会剧增，在时间是处于劣势。但是它具有显著的优点：

• 每一回合中几乎所有的样本皆用于训练模型,因此最接近原始样本的分布,这样评估所得的结果比较可靠。
• 实验过程中没有随机因素会影响实验数据,确保实验过程是可以被复制的。

2、k折交叉验证  K-fold Cross Validation(记为K-CV)

K折交叉验证是以部分代价去获得去一法的大部分收益，这里的k折是吧数据分为k组。它的做法是将k-1组作为训练集训练出一个模型，然后将剩下的一组用做测试集。利用这k个模型最终的平均正确率来衡量模型的正确率。常使用的一般是5折和10折，5折交叉验证是将数据分为5组。实际做法是把20%的数据拿出去作为测试集，将剩下的80%数据训练模型。使用80%或者90%的数据与使用所有数据的效果比较接近。

使用交叉验证时，需要谨慎保持数数据的分布平衡，不能在某一折中全部是一类的数据。

比如有个集合叫data，通常建立机器模型的时候，先对数据进行切分或者选择，取前面80%的数据当成训练集，取20%的数据当成测试集。80%的数据是来建立一个模型，剩下的20%的数据是用来测试模型的表达效果是怎么样的？

• 第一步是将数据进行切分，切分成训练集以及测试集。这部分操作是必须要做的。
• 第二步还要在训练集进行平均切分，比如平均切分成3份，分别是数据集1,2,3。为什么要进行随机的切分呢？因为最终的测试数据集，只能够在一个最终的测试阶段，在模型以及参数都调整好之后，才能用测试集去测试当前模型的效果是怎么样的

在建立模型的时候，不管建立什么样的模型，这个模型伴随着很多参数，有不同的参数进行选择，这个参数选择大比较好，还是选择小比较好一些？从经验值角度来说，肯定没办法很准的，怎么样去确定这个参数呢？只能通过交叉验证的方式。

那什么又叫交叉验证呢？

• 第一次：将数据集1,2分别建立模型，用数据集3在当前权重下一个验证的效果。数据集3是个验证集，验证集是训练集的一部分。用验证集去收集模型是好还是坏？
• 第二次：将数据集1,3分别建立模型，用数据集2在当前权重下一个验证的效果。
• 第三次：将数据集2,3分别建立模型，用数据集1在当前权重下一个验证的效果。

为什么要验证模型3次呢？其实这些操作并非是重复的，每一次的训练集是不一样的。(比如第一次的训练集是1和2，第二次的训练集是1和3，第三次的训练集是3和2)此外验证集也是不一样的。(比如第一次的验证集是3，第二次的验证集是2，第三次的验证集是1)

现在是比较求稳的操作，如果只是求一次的交叉验证，这样的操作会存在风险。比如只做第一次交叉验证，会使3验证集偏简单一些。会使模型效果偏高，此外模型有些数据是错误值以及离群值，如果把这些不太好的数据当成验证集，会使模型的效果偏低的。模型当然是不希望偏高也不希望偏低，那就需要多做几次交叉验证模型，求平均值。这里有1，2，3分别求验证集，每个验证集都有评估的标准。最终模型的效果将1,2,3的评估效果加在一起,再除以3，就可以得到模型一个大致的效果。

交叉验证只是做一步求稳的操作，要让模型的评估效果是可信的。既不能偏高也不能偏低，就这样求了平均值来当模型的效果。

之前说到要做数据交叉验证，要对原始数据集进行切分。sklearn.model_selection是交叉验证模块，train_test_split对原始数据集有进行切分的操作。test_size = 0.3实际做法是把30%的数据拿出去作为测试集，将剩下的70%数据训练模型。这个可以根据实际需求进行修改。

random_state = 0，为了使训练集以及测试集一样，设置随机状态为0，这样就抛开了样本对模型的影响。(之前有对原始数据集进行洗牌，再切分测试集以及训练集，才能保证随机切分。)

X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.3, random_state = 0)
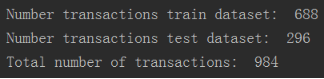
print("Number transactions train dataset: ", len(X_train))
print("Number transactions test dataset: ", len(X_test))
print("Total number of transactions: ", len(X_train)+len(X_test))

上段代码是对所有数据进行处理：X_train,代表的是所有数据的70%作为训练集，X_test表示所有数据的30%作为测试集, y_train表示训练集的标签, y_test表示测试集的标签。之前做了下采样的数据集，让0和1都比较少，要对下采样数据集进行的交叉切分相同的操作。

X_train_undersample, X_test_undersample, y_train_undersample, y_test_undersample = train_test_split(X_undersample,y_undersample ,test_size = 0.3,random_state = 0)
print("Number transactions train dataset: ", len(X_train_undersample))
print("Number transactions test dataset: ", len(X_test_undersample))
print("Total number of transactions: ", len(X_train_undersample)+len(X_test_undersample))

为什么同时要对下采样以及原始的数据进行交叉切分呢?

现在要拿下采样的数据进行模型训练的操作,但是模型训练完要进行测试,那么测试的时候拿什么数据集进行测试呢?

是拿下采样切分的测试数据集进行测试么?因为下采样切分的测试数据数量比较少,不具备原始数据的分布规则.最终的测试集是拿原始数据集中的测试数据集再进行测试.

因此这里有2种切分的方式,第一种是对原始数据集即28万个数据进行交叉切分.然后有对984个下采样数据集又进行了一次交叉切分,

后面会拿原始数据中的85443的数据集进行测试操作。而下采样的数据总共有984个,训练集的数据共有668个,测试集有296个,上面已经将数据集进行了切分,就可以进行建模的操作,在建模的过程中要使用逻辑回归.

模型评估方法

假设有1000个病人的数据,要对1000个病人进行分类,有哪些是癌症的?哪些不是患有癌症的?

假设有990个人不患癌症,10个人是患癌症.用一个最常见的评估标准,比方说精度,就是真实值与预测值之间的差异.真实值用y来表示,预测值用y1来表示.y真实值1,2,3...10,共有10个样本,y1预测值1,2,3...10,共有10个样本.精度就是看真实值y与预测值y1是否一样的.要么都是0,要么都是1,如果是一致,就用=表示,比如1号真实值样本=预测值的1号样本,如果不相等就用不等号来表示.如果等号出现了8个,那么它的精确度为8/10=80%,从而确定模型的精度.

990个人不患癌症,10个人是患癌症建立一个模型,所有的预测值都会建立一个正样本.对1000个样本输入到模型,它的精确度是多少呢?990/1000=99%

这个模型把所有的值都预测成正样本,但是没有得到任何一个负样本.在医院是想得到癌症的识别,但是检查出来的结果是0个,虽然精度达到了99%,

但这个模型是没有任何的含义的,因为一个癌症病人都找不出来.在建立模型的时候一定要想好一件事,模型虽然很容易建立出来,那么难点是应该怎么样去评估这样的模型呢?

刚才提到了用精度去评估模型,但是精度有些时候是骗人的.尤其是在样本数据不均衡的情况下.

接下来要讲到一个知识点叫recall,叫召回率或叫查全率.recall有0或者1,我们的目标是找出患有癌症的那10个人.因此根据目标制定衡量的标准.就是有10个癌症病人,能够检测出来有几个?如果检测0个癌症病人,那么recall值就是0/10=0;如果检测2个癌症病人,那么recall值就是2/10=20%.用recall检测模型的效果更科学一些.

建立模型无非是选择一些参数,如果精度专用recall来表示,也并非那么容易.在统计学中会经常提到的4个词,分别如下:

• True positive:正确的判断成正类
• False positive:错误地判断成了正类，把负类判断成正类
• False negative:错误的判断成负类，本来是正类
• True negative:正确的判断成负类。

比如一个班级有80个男生,20个女生,共100个人,在100多个人中有个目标,把所有的女生都抓出来.建立一个模型,挑选50个人,预测结果是20个是女的,剩下30个是男的. TP:表示预测对的正例结果,比如判断成正例,20个女生,当成正例. FP:表示预测错的正例结果,把负例判断成正例,比如把男生判断成女生,共有30个. FN:就是把女生错当成男生的例子为0个. TN:就是把男生判断成了男生,因此等于50.

这里的Recall = TP/(TP+FN)

正则化惩罚项

先导入机器学习建模的库

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold, cross_val_score
from sklearn.metrics import confusion_matrix,recall_score,classification_report

这里的KFold是指交叉验证的时候,可以选择做几倍的交叉验证.之前有提到将原始的训练集切分成3份,不光可以切分成3份,也可以切分成4份或者5份都可以的,可以根据自己的喜好,任意的切分.

cross_val_score值是指交叉验证评估得到的结果,confusion_matrix是混淆矩阵

在机器建模的时候需要做这样的一件事,要做交叉验证,要把原始的数据集切分成几部分,fold = KFold(len(y_train_data),5,shuffle=False) ,这里将原始数据传进来,并切分成了5部分.

在逻辑回归当中,需要有写参数传进来,今天的参数叫做正则化惩罚项,什么叫正则化惩罚?

比如有A模型：，比如还有B模型，这两个模型的recall值都是等于90%。如果两个模型的recall值都是等于90%，是不是随便选一个都可以呢？

比如A模型的原点浮动比较大，具体如截图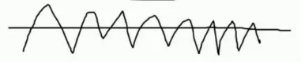：比如B模型的原点浮动比较小，具体如截图：虽然两个模型的recall值都是等于90%，A模型的浮动范围太大了，都希望模型更加稳定一些，不光满足训练的数据，还要尽可能的满足测试数据。因此希望模型的浮动差异更小一些，差异小可以使过度拟合的风险更小一些。

过度拟合的意思是在训练集表达效果很好，但是在测试集表达效果很差，因此这组模型发生了过拟合。过拟合是非常常见的现象，很大程度上是因为权重参数浮动较大引起的，因此希望得到B模型，因为B模型的浮动差异比较小。

那么怎么样能够得到B模型呢？从而就引入了正则化的东西，惩罚模型的，因为模型的数据有时候分布大，有时候分布小。希望大力度惩罚A模型，小力度惩罚B模型，可不可以呢？

L2正则化

首先介绍一些L2正则化，对于目标损失函数来说，希望目标函数是越低越好的，在惩罚的过程中，需要在(loss)损失目标函数中+1/2w*w，即就是如下截图：

对于A模型，值浮动比较大，如果计算的话，这样的话计算的目标损失函数的值就会更大。对于B模型而言，计算的目标损失函数的值也是如此。

分别计算A、B模型中的中的值，哪个值更加低？

L1正则化

(loss)损失目标函数中+|w|，去计算当前的惩罚力度是多少？

因此有两种惩罚函数，一种是L2正则化，一种是L1正则化。在判断之前需要设置好参数，需要设置当前惩罚的力度有多大？可以设置成0.1惩罚力度比较小，也可以设置惩罚力度为1，也可以设置惩罚力度为10。但是惩罚力度等于多少的时候，效果比较好呢？具体多少也不知道，需要通过交叉验证，去评估一下什么样的参数达到更好的效果。

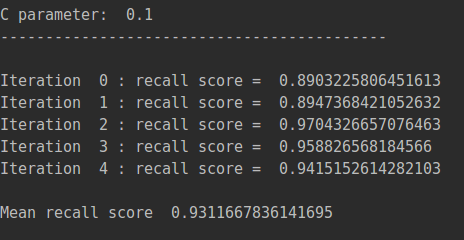
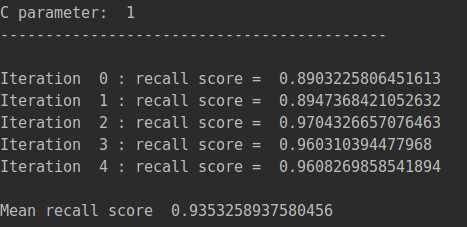
c_param_range = [0.01,0.1,1,10,100]这里就是前面提到的那一章的惩罚力度。需要将这5个参数不断的尝试。

这一部分内容是可视化显示，具体如下：

results_table=pd.DataFrame(index=range(len(c_param_range),2),columns=['C_parameter','Mean recall score'])
results_table['C_parameter'] = c_param_range

下面来看下完整的代码：

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold, cross_val_score
from sklearn.metrics import confusion_matrix,recall_score,classification_report

def printing_Kfold_scores(x_train_data,y_train_data):
    fold = KFold(5,shuffle=False,random_state=0)
    c_param_range = [0.01,0.1,1,10,100]
    results_table = pd.DataFrame(index = range(len(c_param_range),2), columns = ['C_parameter','Mean recall score'])
    results_table['C_parameter'] = c_param_range
    #print("可视化惩罚力度:",results_table)
    j = 0
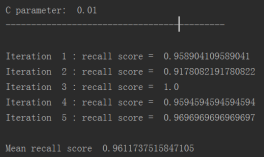
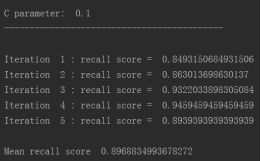
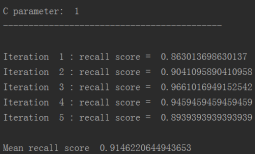
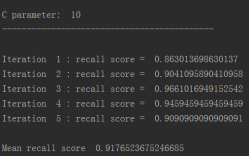
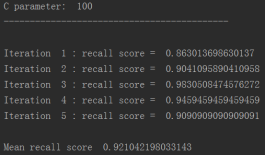
    for c_param in c_param_range:
        print('-------------------------------------------')
        print('C parameter: ', c_param)
        print('-------------------------------------------')
        print('')
        recall_accs = []
        for iteration, indices in enumerate(fold.split(x_train_data)):
            lr = LogisticRegression(C = c_param, penalty = 'l1')
            lr.fit(x_train_data.iloc[indices[0],:],y_train_data.iloc[indices[0],:].values.ravel())
            y_pred_undersample = lr.predict(x_train_data.iloc[indices[1],:].values)
            recall_acc = recall_score(y_train_data.iloc[indices[1],:].values,y_pred_undersample)
            recall_accs.append(recall_acc)
            print('Iteration ', iteration,': recall score = ', recall_acc)
        # The mean value of those recall scores is the metric we want to save and get hold of.
        results_table.ix[j,'Mean recall score'] = np.mean(recall_accs)
        j += 1
        print('')
        print('Mean recall score ', np.mean(recall_accs))
        print('')

best_c = printing_Kfold_scores(X_train_undersample,y_train_undersample)

lr = LogisticRegression(C = c_param, penalty = 'l1')首先建立逻辑回归模型,在逻辑回归函数,传进C这个惩罚力度参数.惩罚的方式可以选择l1惩罚或者l2惩罚.

lr.fit(x_train_data.iloc[indices[0],:],y_train_data.iloc[indices[0],:].values.ravel())这个语句是对模型进行训练,用交叉验证的方式建立一个模型.

y_pred_undersample = lr.predict(x_train_data.iloc[indices[1],:].values),建立完模型之后就可以进行预测.

比如在C=0的情况下,它的效果是多少的?并计算recall的值, 从结果可以看出，当惩罚参数是0.01时，recall值最高。

混淆矩阵

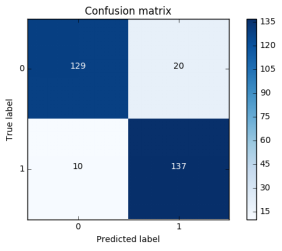混淆矩阵是由一个坐标系组成的,有x轴以及y轴,在x轴里面有0和1,在y轴里面有0和1.x轴表达的是预测的值,y轴表达的是真实的值.可以对比真实值与预测值之间的差异,可以计算当前模型衡量的指标值.

之前有提到recall=TP/(TP+FN),在这里的表示具体如下: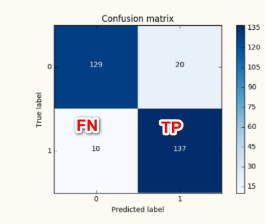这里也可以衡量精度等于多少?

真实是0,预测也是0,等到的结果是129;真实是1,预测也是1,等到的结果是137.精确度=(129+137)/(129+20+10+137) 从上面可以看出,混淆矩阵可以看出一些指标.比如精确值以及recall值.

我们来看下代码：

#混淆矩阵
def plot_confusion_matrix(cm, classes,title='Confusion matrix',cmap=plt.cm.Blues):
    """
    This function prints and plots the confusion matrix.
    """
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, rotation=0)
    plt.yticks(tick_marks, classes)
    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, cm[i, j],
                 horizontalalignment="center",
                 color="white" if cm[i, j] > thresh else "black")

    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')

#采用下样本
import itertools
lr = LogisticRegression(C = 0.01, penalty = 'l1')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred_undersample = lr.predict(X_test_undersample.values)

# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test_undersample,y_pred_undersample)
#print("TP,NP,TF,NF的值输出，并且输出的是一个矩阵:",cnf_matrix)
np.set_printoptions(precision=2)

print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))

# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Confusion matrix')
plt.show()

这里我们主要是要求出recall的值，第一个函数plot_confusion_matrix()的功能是画出矩阵。

下面我们用LogisticRegression函数预测出测试集的标签，然后将预测的标签结果和真实的测试集的标签进行比较，得出矩阵的TP,NP,TN,FN值。然后通过recall的公式(TP/TP+NP),计算出recall值。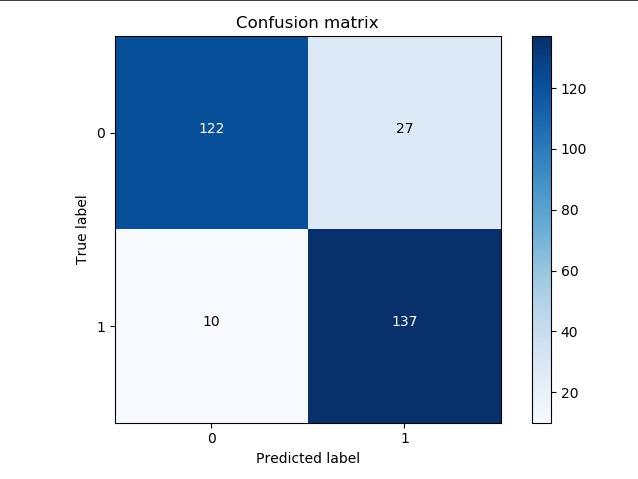混淆矩阵是在什么样的条件下进行计算的呢?在下采样数据集,样本数量比较小,大概有200多个样本,进行小规模的测试,还没有在大规模的数据进行测试.

其实之前有提到,数据衡量的时候应该在原始的数据集上,所以不光只在下采样数据集进行测试,还要在原始的数据集进行测试.原始的数据大概有8万多条数据,因此还要在原始的数据集进行操作.

代码如下：

#采用全部样本
lr = LogisticRegression(C = 0.01, penalty = 'l1')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred = lr.predict(X_test.values)
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test,y_pred)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Confusion matrix')
plt.show()

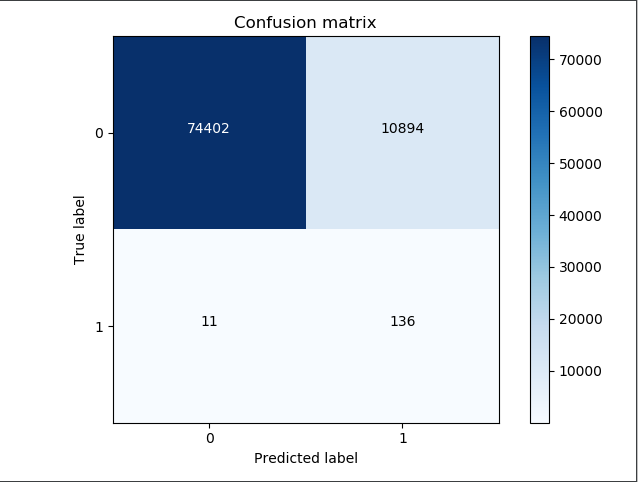首先我们计算原始数据的recall值, recall=TP/(TP+FN)=136/(136+11)=91%,recall值比较偏高.

这里的recall值偏高,那这里的数据有没有什么问题呢?对角线的数据74402以及136都是预测对的数据.这里的10894指的是本来没有异常发生的,然后误抓出来了,为了检测到136个样本,把额外的10894个样本也抓出来了,说它也是异常的.这种情况下,显然不会影响我们的recall值,但是会使精度偏低,从实际的角度来看,使我们的工作量也增大了,虽然找出了136个欺诈行为的样本,但是也找出了10894个无辜的样本.

找出样本之后,需要对实际进行分析,确保确实是异常的,但是有10894个无辜的样本,那应该怎么办呢?因此下采样数据,虽然recall值能够达到标准,但是误杀有点太多.这个误杀已经超过容忍范围,那应该怎么解决这个问题呢?下采样会出现这样的问题,那么过采样是否效果会更好一些呢?

刚才用了下采样数据集进行了建模的操作,然后得到一些recall的结果值.如果对一个数据集的0和1什么都不做,直接拿出来模型的建立,效果到底会有多差呢?效果到底是怎么样的呢?如果不用过采样以及下采样,直接拿原始的数据集进行交叉验证.

从输出结果可以看出,在样本数据不均衡的情况下,如果什么都不做,模型的效果是不如下采样的模型数据集.这里的recall值只有62%,模型效果并不好.

逻辑回归阈值对结果的影响

在当前的指标下,去做逻辑回归,有做阈值得到一个结果,算出其中的recall值,能不能使得模型的评估标准可以进行人为的控制一下呢?还是要回到Logistic函数.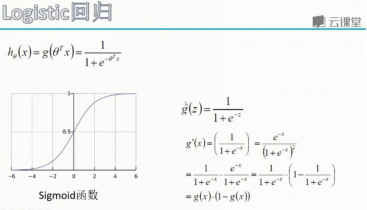之前有提到案例比如,0.7>0.5是1类别,0.4<0.5是0类别,那我能不能通过一个改变,这个0.5是谁制定的呢?好像是系统默认的,把0.5当成是一个平均值.那能不能将0.5人为的做一些变化呢?

当然也是可以的.

比如在sigmoid函数上画一条横线,具体如下: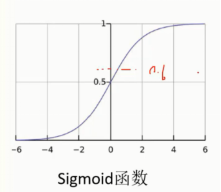为了让标准更加严格一些,只有>0.6才预测成1类,比如:0.7>0.6预测成1类,0.55<0.6预测成0类.

当前模型最终的一个结果是可以人为可控的,可以自己设置一些阈值,我们把刚才y=0.6,这个叫自定义阈值. 如果将这个阈值自定义成y=0.9,那么筛选就会更加严格一些,只有那些具备异常可能性的,才把它当成一个异常的.

如果把阈值放低一些,那么这种情况下就相当于宁可错杀一万也不放过一个的感觉.对于样本而言,不管它的预测值是什么样的?比如y=0.1,只要>0.1就设置为异常. 那么在python中怎么样认为的设置阈值呢?

之前在python中预测值的设置是类别值，代码如下：

y_pred_undersample=Ir.predict(X_test.values)

现在预测的是相当于概率值，代码如下：

y_pred_undersample_proba=Ir.predict_proba(X_test_undersample.values)

有了概率值可以跟指定的一系列阈值进行比较。

完整的代码如下：

lr = LogisticRegression(C=0.01, penalty='l1')
lr.fit(X_train_undersample, y_train_undersample.values.ravel())
y_pred_undersample_proba = lr.predict_proba(X_test_undersample.values)



thresholds = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]

plt.figure(figsize=(10, 10))

j = 1
for i in thresholds:

    y_test_predictions_high_recall = y_pred_undersample_proba[:, 1] > i

    plt.subplot(3, 3, j)
    j += 1

    # Compute confusion matrix
    cnf_matrix = confusion_matrix(y_test_undersample, y_test_predictions_high_recall)
    np.set_printoptions(precision=2)

    print("Recall metric in the testing dataset: ", cnf_matrix[1, 1] / (cnf_matrix[1, 0] + cnf_matrix[1, 1]))

    # Plot non-normalized confusion matrix
    class_names = [0, 1]
    plot_confusion_matrix(cnf_matrix , classes=class_names, title='Threshold >= %s' % i)
    plt.show()

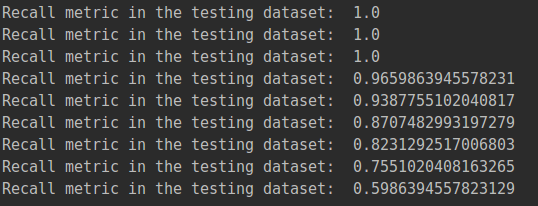
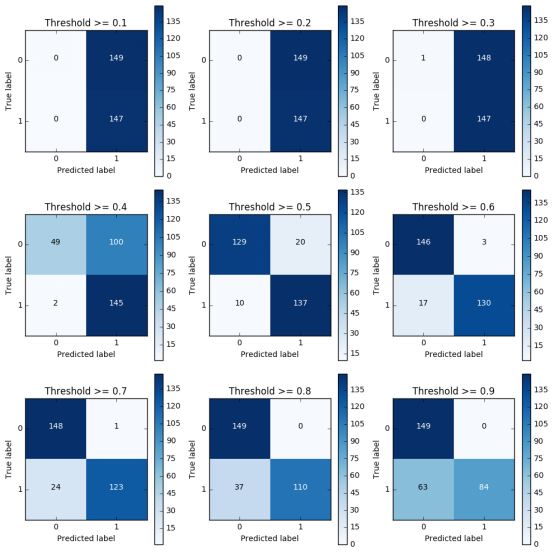通过结果可以看出,随着阈值的上升,它的recall值的变化,recall值由1.0下降到0.57.图上可以看出,不同的阈值, 混淆矩阵是长什么样子的.

• 阈值>=0.1 它的recall值是147/(147+0),当前检测的样本所有的异常值都检查到了.而误杀值149.精度很低,评估一个模型的时候需要多层次进行评估.不能把所有的样本都预测成异常样本.

• 阈值>=0.2以及阈值>=0.3 它的recall值是满的,精度值还是很低.

• 阈值>=0.4以上 误杀值越来越少,精度偏高了一些.但是阈值设置太大也不可以,比如阈值>=0.9,要求太严了,有些就检测不到了.recall值就会偏低,只有大约60%左右.只有阈值>=0.5的结果看起来不错.

在实际回归进行建模的时候,也要从实际的角度进行出发,阈值应该怎么进行一个设定.比如误杀率不能高于百分之十,然后可以根据自己的实际需求去选择这些参数.

SMOTE样本生成策略

对于下采样操作而言,模型回归的评估以及参数的选择.那么这个就是下采样应该怎么样去做这个事情.不光有下采样的操作,还有过采样的操作.那么接下来讲的就是过采样的操作,是关于SMOTE的算法.

• 对于少数类中每一个样本x，以欧氏距离为标准计算它到少数类样本集中所有样本的距离，得到其k近邻.
• 根据样本不平衡比例设置一个采样比例以确定采样倍率N，对于每一个少数类样本，从其k近邻中随机选择若干个样本,假设选择的近邻为. (3)对于每一个随机选出的近邻，分别与原样本按照如下的公式构建新的样本.

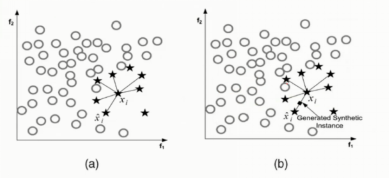在过采样的时候要有数据的生成,现在有0和1两类的样本.0类样本很多,1类样本很少,现在希望1类的样本也很多进行生成的操作.

首先导入python相关的库以及模块

import pandas as pd
from imblearn.over_sampling import SMOTE
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split

# coding:utf-8
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix,recall_score,classification_report
from sklearn.model_selection import train_test_split

credit_cards=pd.read_csv('creditcard.csv')
columns=credit_cards.columns
features_columns=columns.delete(len(columns)-1)
#print("只输出特征:\n",features_columns)
features=credit_cards[features_columns]
#print("输出特征:\n",features)
labels=credit_cards['Class']
#print("打印数据的标签:\n",labels)
features_train, features_test, labels_train, labels_test = train_test_split(features, labels, test_size=0.2, random_state=0)

我们来看下重点的代码，具体如下：

oversampler=SMOTE(random_state=0)
os_features,os_labels=oversampler.fit_sample(features_train,labels_train)

fit_sample(features_train,labels_train)传进来的是训练集的x以及训练集的y,训练完之后,就会自动做一个平衡,就会知道0有多少个,1有多少个?

len(os_lables[os_labels==1])

这里是计算lable1的有多少个?共有227454个.lable0的也有20多万个,因此样本就均衡了.可以通过过采样的方式,查看recall有多少.

os_features=pd.DataFrame(os_features)
os_labels=pd.DataFrame(os_labels)
best_c=printing_Kfold_scores(os_features,os_labels)

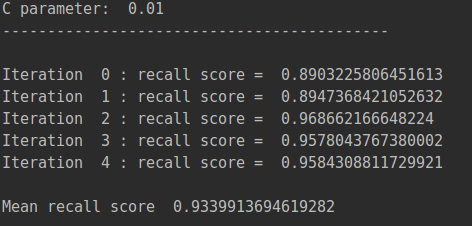
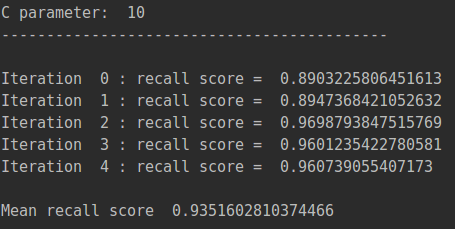
通过调用之前写的printing_Kfold_scores函数，得出recall值。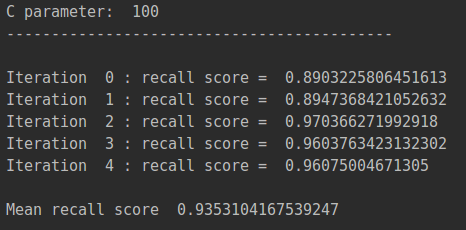我么再来看下混淆矩阵

lr = LogisticRegression(C = best_c, penalty = 'l1')
lr.fit(os_features,os_labels.values.ravel())
y_pred = lr.predict(features_test.values)

# Compute confusion matrix
cnf_matrix = confusion_matrix(labels_test,y_pred)
np.set_printoptions(precision=2)

print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))

# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
                      , classes=class_names
                      , title='Confusion matrix')
plt.show()

输出结果如下：

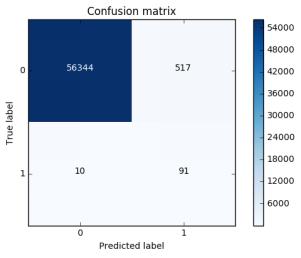
通过输出结果我们可以知道,测试集共有5万多个样本,recall值是等于90%.之前的recall值是约等于91%(这个数值是大概,有点忘记了).这个结果比之前的结果稍微低了一些,而现在的误杀值有517个.之前的误杀值有8000多个,是500多个的十几倍.通过过采样得到的误差是偏低一些的.

使用过采样recall值可能偏低一些,但是模型的优点是精度偏高.这就是与下采样的区别.

总结

对于样本不均衡数据,要利用越多的数据越好,能利用一种生成方式,就不妨利用这种生成方式.下采样误杀率很高,这是模型本身自带的一个问题,因为0和1一样少,会存在潜在的意识是原始数据0和1的数据一样少,导致误杀率偏高.过采样的结果偏好一些,虽然recall偏低了一点,但是整体的效果还是不错的.

流程总结:

首先要观察数据,当前数据是否分布均衡,不均衡的情况下就要想一些方法.

这次的数据是比较纯净的,不需要做其他一些预处理的操作,可以直接拿来使用.很多情况下,不见得可以直接拿到特征数据,

如果遇到一些没有被处理好的数据，我们就需要做特征工程。让数据进行标准化,让数据的浮动比较小一些,然后再进行数据的选择以及参数的选择.通过交叉验证的方式.

混淆矩阵以及模型的评估标准 通过阈值与预测值进行比较,然后得到最终的一个预测结果.不同的阈值会使结果发生很大的变化.

面试可能问到的问题

1.推导一下逻辑回归算法，如何得到损失函数

对数似然公式为：

我们要求其最大值，所以引入转换为梯度下降任务，求其最小值。

所以现在公式变为：

求平均损失：

2.逻辑回归解决的是二分类模型，多分类模型是softmax(学习DL的根据)

3.是否了解SGD中的二阶优化算法、学习率会对这个算法有什么影响

梯度下降法主要分为三种：

• 梯度下降法
• 随机梯度下降
• 小批量梯度下降

梯度下降法：

梯度下降使用整个训练数据集来计算梯度，因此它有时也被称为批量梯度下降

下面就以均方误差讲解一下，假设损失函数为：

其中是预测值，是真实值，那么要最小化上面损失,需要对每个参数运用梯度下降法：

其中，是损失函数对的偏导数，是学习率，也是每一步更新的步长。

随机梯度下降法：在机器学习/深度学习中，目标函数的损失函数通常取各个样本损失函数的平均，那么假设目标函数为：

其中，是第个样本的目标函数，那么目标函数在处的导数为：

如果使用梯度下降法(批量梯度下降法)，那么每次迭代过程中都要对n个样本进行求梯度，所以开销非常大。随机梯度下降的思想就是随机采样一个样本来更新参数，那么计算开销就从下降到

小批量梯度下降法：随机梯度下降虽然提高了计算效率，降低了计算开销，但是由于每次迭代只随机选择一个样本，因此随机性比较大，所以下降过程中非常曲折。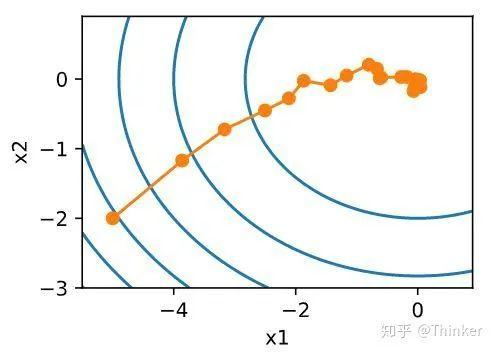所以，样本的随机性会带来很多噪声，我们可以选取一定数目的样本组成一个小批量样本，然后用这个小批量更新梯度，这样不仅可以减少计算成本，还可以提高算法稳定性。小批量梯度下降的开销为 其中是批量大小。

先写这么多吧，白天实习，晚上再补算法，心力交瘁！

参考文献

1.如何理解随机梯度下降