Java详解剑指offer面试题38--字符串的排列
Java详解剑指offer面试题38–字符串的排列
输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。
注意这道题求得是全排列。求若干字符组成的序列的所有排列可能,可以将字符序列分解成两部分:
- 第一个字符
- 第一个字符之后的字符序列
这样就把一个大问题分解成了小问题,然后对小问题继续采用相同的策略即可!
因为所有字符都可能处于第一个位置,我们可以把第一个字符和其后的所有字符交换位置,这样就保证了所有字符都会位于第一个字符处;交换后固定第一个字符,然后对于其后的字符序列,继续分成两部分:第一个字符和其后的字符序列…这是一个递归过程!
第一个字符和其后的所有字符依次交换位置可以用一个for循环完成,对于循环中的每一次交换:在交换位置后要对除第一个字符外的字符序列进行递归。**这里一定要注意,第一个字符首先要和自己交换一下。**一次递归调用结束后,需要将之前的交换复原,以保证下次交换依然是和第一个字符交换。比如abcd,第一个字符和第二个字符交换后变成bacd,此后固定b对acd递归,递归结束后,需要将bacd复原成abcd,以便下次a和c交换位置变成cbad…
实现如下
package Chap4;
import java.util.ArrayList;
import java.util.Collections;
/**
* 通用的根据输入字符串得到全排列的程序,排序是为了保证字典序
*/
public class Permutation {
public ArrayList<String> permutation(String str) {
ArrayList<String> list = new ArrayList<>();
if (str == null || str.length() == 0) {
return list;
}
collect(str.toCharArray(), 0, list);
// 保证字典序
Collections.sort(list);
return list;
}
private void collect(char[] chars, int begin, ArrayList<String> list) {
if (begin == chars.length - 1) {
// 不能存入相同的排列
String s = String.valueOf(chars);
if (!list.contains(s)) {
list.add(s);
return;
}
}
for (int i = begin; i < chars.length; i++) {
swap(chars, i, begin);
collect(chars, begin + 1, list);
swap(chars, i, begin);
}
}
private void swap(char[] chars, int i, int j) {
char temp = chars[j];
chars[j] = chars[i];
chars[i] = temp;
}
public static void main(String[] args) {
Permutation a = new Permutation();
System.out.println(a.permutation("gba"));
}
}
上述思路体现在了递归方法collect的for循环中,将一种排列存入的时机是当begin移动到字符串末尾的时候,输入的字符序列可能含有相同的字符,这样会产生重复的排列,我们当然不希望所有全排列的可能中有重复的序列。因此存入list之前需要判断list是否已经包含了该序列。递归的过程可以用下面的树结构来加深理解,该函数的递归过程就是树的前序遍历顺序,在叶子结点处会将该排列存入list中。红色的字符是被交换过的字符,绿色的字符则没有经过交换。注意本题并没有树的数据结构,只不过这个类比可以帮助我们更好的理解整个递归过程。
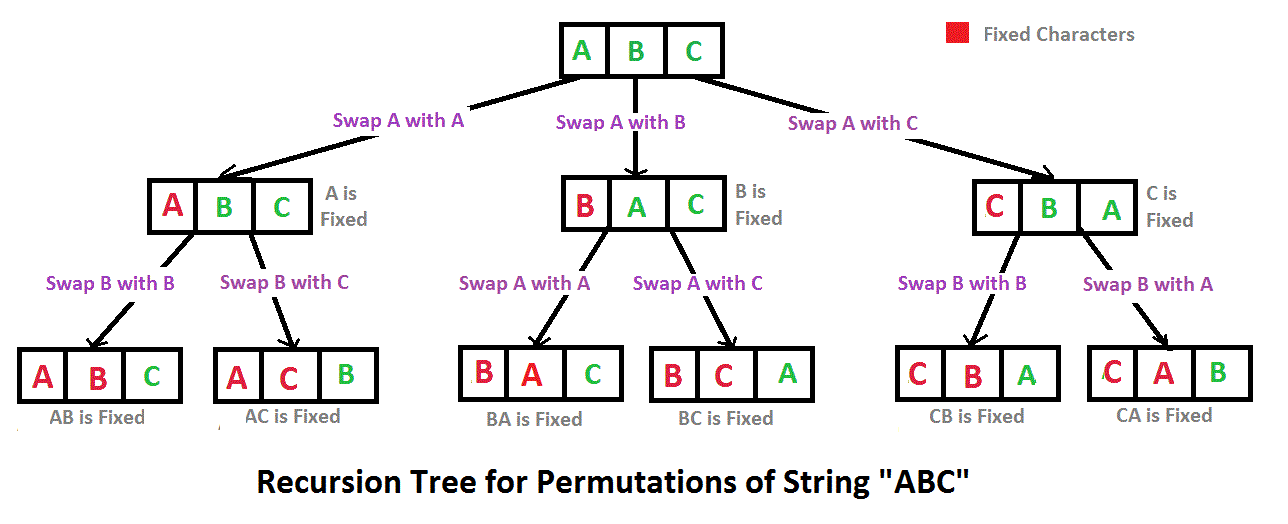
最后得到了所有的全排列[ABC, ACB, BAC, BCA, CBA, CAB],其实这样就可以了,不过题目要求以字典序输出,那就再排序一下吧,内置的sort方法默认就是以字典序来排序的。
字符串的组合
如果要求字符的所有组合呢?比如abc,所有组合情况是[a, b, c, ab, ac, bc, abc],包含选择1个、2个、3个字符进行组合的情况,即
∑
C
3
1
+
C
3
2
+
C
3
3
\sum{C_3^1 + C_3^2 + C_3^ 3}
∑C31+C32+C33。这可以用一个for循环完成。所以关键是如何求得在n个字符里选取m个字符总共的情况数,即如何求C(n, m)
n个字符里选m个字符,有两种情况:
- 第一个字符在组合中,则需要从剩下的n-1个字符中再选m-1个字符;
- 第一个字符不在组合中,则需要从剩下的n-1个字符中选择m个字符。
上面表达的意思用数学公式表示就是
C n m = C n − 1 m − 1 + C n − 1 m C_n^m = C_{n-1}^{m-1} + C_{n-1}^m Cnm=Cn−1m−1+Cn−1m
基于这个公式,就可实现如下递归程序。
package Chap4;
import java.util.*;
/**
* 求字符的所有排列,允许组合中有重复元素
*/
public class Combination {
/**
* 其实就是求C(n, m) 其中n == str.length; m == num
*
* @param str 字符序列
* @param num 选几个字符进行组合
* @return C(n, m)的集合
*/
public List<String> combinationAccordingToNum(String str, int num) {
List<String> list = new ArrayList<>();
if (str == null || str.length() == 0 || num > str.length()) {
return list;
}
StringBuilder sb = new StringBuilder();
collect(str, sb, num, list);
return list;
}
/**
* 求所有组合情况
*/
public List<String> combination(String str) {
List<String> list = new ArrayList<>();
if (str == null || str.length() == 0) {
return list;
}
StringBuilder sb = new StringBuilder();
// 收集字符个数为i的组合
for (int i = 1; i <= str.length(); i++) {
collect(str, sb, i, list);
}
return list;
}
private void collect(String str, StringBuilder sb, int number, List<String> list) {
// 两个if顺序不可交换,否则C(n, n)不会存入到list中:即collect("", sb, 0)时,要先判断num==0存入后,再判断str.length ==0决定不再递归
if (number == 0) {
if (!list.contains(sb.toString()))
list.add(sb.toString());
return;
}
// 当str为""时候直接返回,不然下一句charAt(0)就会越界
if (str.length() == 0) {
return;
}
// 公式C(n, m) = C(n-1, m-1)+ C(n-1, m)
// 第一个字符是组合中的第一个字符,在剩下的n-1个字符中选m-1个字符
sb.append(str.charAt(0)); // 第一个字符选中
collect(str.substring(1), sb, number - 1, list);
sb.deleteCharAt(sb.length() - 1); // 取消选中第一个字符
// 第一个字符不是组合中的第一个字符,在剩下的n-1个字符中选m个字符
collect(str.substring(1), sb, number, list);
}
public static void main(String[] args) {
Combination c = new Combination();
System.out.println(c.combination("abcca"));
System.out.println(c.combination("abc"));
System.out.println(c.combinationAccordingToNum("aabbc", 2));
}
}
上面的公式体现在了collect递归方法中,number就表示了要从字符序列中选择m个字符进行组合。每调用一次collect方法,number就要减1,当number等于0时,说明已经收集了m个字符,将该组合情况存入list中。
排列的应用–正方体的八个顶点
输入一个含有8个数字的数组,判断有没有可能吧这8个数字分别放到正方体的8个顶点,使得正方体三对相对的面上的4个顶点的和相等
8个数字放在8个顶点上,总共有 A 8 8 A_8^8 A88种情况,先求得这八个数字的全排列,然后从中筛选出满足给定条件的的排列即可。
package Chap4;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/**
* 通用的根据数组输入得到全排列的程序
*/
public class PermutationExt {
/**
* 应用排列解决问题1:输入一个含有8个数字的数组,
* 判断有没有可能吧这8个数字分别放到正方体的8个顶点,使得正方体三对相对的面上的4个顶点的和相等
*/
public List<int[]> possibilitiesOfCube(int[] array) {
List<int[]> list = new ArrayList<>();
if (array == null || array.length == 0) {
return list;
}
// 得到全排列集合
List<int[]> all = permutation(array);
// 筛选:满足三个对立面的值相等才会被加入最终结果集中
for (int[] arr : all) {
if (checkSum(arr)) list.add(arr);
}
return list;
}
public List<int[]> permutation(int[] array) {
List<int[]> list = new ArrayList<>();
collect(array, 0, list);
return list;
}
private void collect(int[] array, int begin, List<int[]> list) {
if (begin == array.length - 1) {
// list中没有同样的序列
if (!has(list, array)) {
// 必须使用副本,不能直接传入引用,否则list所有的int[]对象最后都一样
list.add(Arrays.copyOf(array, array.length));
return;
}
}
for (int i = begin; i < array.length; i++) {
swap(array, i, begin);
collect(array, begin + 1, list);
swap(array, i, begin);
}
}
private boolean checkSum(int[] array) {
if ((array[0] + array[2] + array[4] + array[6] == array[1] + array[3] + array[5] + array[7]) &&
(array[0] + array[1] + array[2] + array[3] == array[4] + array[5] + array[6] + array[7]) &&
(array[2] + array[3] + array[6] + array[7] == array[0] + array[1] + array[4] + array[5])) {
return true;
}
return false;
}
private boolean has(List<int[]> list, int[] a) {
for (int[] arr : list) {
if (equal(arr, a)) return true;
}
return false;
}
private boolean equal(int[] a, int[] b) {
for (int i = 0; i < a.length; i++) {
if (a[i] != b[i]) return false;
}
return true;
}
private void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
public static void main(String[] args) {
PermutationExt p = new PermutationExt();
int[] a = {8, 3, 5, 4, 1, 2, 5, 6};
List<int[]> list = p.possibilitiesOfCube(a);
System.out.println("有" + list.size() + "种可能");
for (int[] arr : list) {
System.out.println(Arrays.toString(arr));
}
}
}
和字符的排列问题如出一辙,只是将char[]换成了int[]。判断list中是否已经存在某排列,不能直接拿对象作比较,我们这里比较的是两个数组中的内容是否完全一样(包括顺序),equal方法就做了这样的工作。另外list中有多个数组,因此list中每个数组都要和即将存入的数组用equal方法比较一下,直到发现list中某个数组内容和将存入的数组内容相同为止,如果遍历完list中所有数组仍然没有找到某个数组内容和将存入的数组一样,此时才允许将其存入list中。
另外int[]是一个对象,存入list时不能直接存入引用,否则最后list中所有的数组都一模一样。通过permutation(array)方法得到全排列,之后通过checkSum方法筛选满足条件的排列。
排列的应用–八皇后问题
8X8的国际棋盘上,有8个皇后,使其不能相互攻击,即它们不能在同一行、同一列、且同一条对角
如下就是一个满足题目的解

三个条件都要满足,我们可以一一来满足,思路如下:
- 保证不同行:使用一个数组表示不同行的皇后,八个皇后则int[] queens = new int[8],其中queens[i]表示位于第i行的皇后,这保证了皇后们不位于同一行;
- 保证不同列:为queens[i]赋值各不相同的数值,queens[i] = j表示位于i行的皇后也位于j列,每个i赋予了不同的j值保证了不同行的皇后也不位于不同列
- 保证不在同一条对角线:如果在同一条对角线,说明矩形的行数等于列数,即当j > i时:
j - i == queens[j] -queens[i](第j行的皇后在第i行的皇后右下方);或者j - i == queens[i] -queens[j](第j行的皇后在第i行的皇后左下方)
先来满足前两条,很简单只需要初始化一个像下面这样的数组即可,即刚开始将皇后们置于棋盘的对角线上,这当然不是个符合条件的解。
// 大小为8的数组,且数值各不相同,任意排列都保证了不同行不同列
int[] queens = {0, 1, 2, 3, 4, 5, 6, 7};
接下来要做的就是:随意打乱数组的排列顺序,不管怎么打乱始终是满足八皇后不在同一行、同一列的,从所有排列情况中筛选出任意两个皇后都不位于同一条对角线上的那些排列情况。
package Chap4;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class EightQueens {
/* 这又是一个全排列的扩展问题,先求出所有的排列可能,从中排除不符合要求的摆放方法即可
*/
public List<int[]> possibilitiesOfQueensPlaced() {
// 大小为8的数组,且数值各不相同,任意排列都保证了不同行不同列
int[] queens = {0, 1, 2, 3, 4, 5, 6, 7};
List<int[]> list = new ArrayList<>();
PermutationExt p = new PermutationExt();
// 得到全排列
List<int[]> all = p.permutation(queens);
// 筛选
for (int[] arr : all) {
if (!isLocatedSameDiagonal(arr)) list.add(arr);
}
return list;
}
/**
* 检查任意两个皇后是否在同一条对角线上
*/
private boolean isLocatedSameDiagonal(int[] queens) {
for (int i = 0; i < queens.length; i++) {
for (int j = i + 1; j < queens.length; j++) {
if (j - i == queens[j] - queens[i] || j - i == queens[i] - queens[j]) {
return true;
}
}
}
return false;
}
public static void main(String[] args) {
EightQueens queens = new EightQueens();
List<int[]> l = queens.possibilitiesOfQueensPlaced();
System.out.println("共有" + l.size() + "种放置方法");
for (int[] arr : l) {
System.out.println(Arrays.toString(arr));
}
}
}
这是个经典的问题,可以记住答案是92。
本文参考文献:
[1]github.com/haiyusun/data-structures