一文让你轻松理解读懂KNN分类算法~
点击上方“码农的后花园”,选择“星标” 公众号
精选文章,第一时间送达
1968年由 Cover和Hart提出最近邻(K-Nearest Neighbors, KNN)算法,KNN是机器学习中有监督学习的一种分类算法,与另外一个机器学习中的无监督学习算法Kmeans类似,但是有本质区别。KNN应用场景有字符识别、 文本分类、 图像识别等领域。
K最近邻分类算法,或者说邻近算法是数据挖掘分类技术中最简单的方法之一。所谓K最近邻就是K个最近的邻居的意思,说的是每个样本都可以用它最接近的K个邻近值来代表。近邻算法就是将数据集合中每一个记录进行分类的方法。
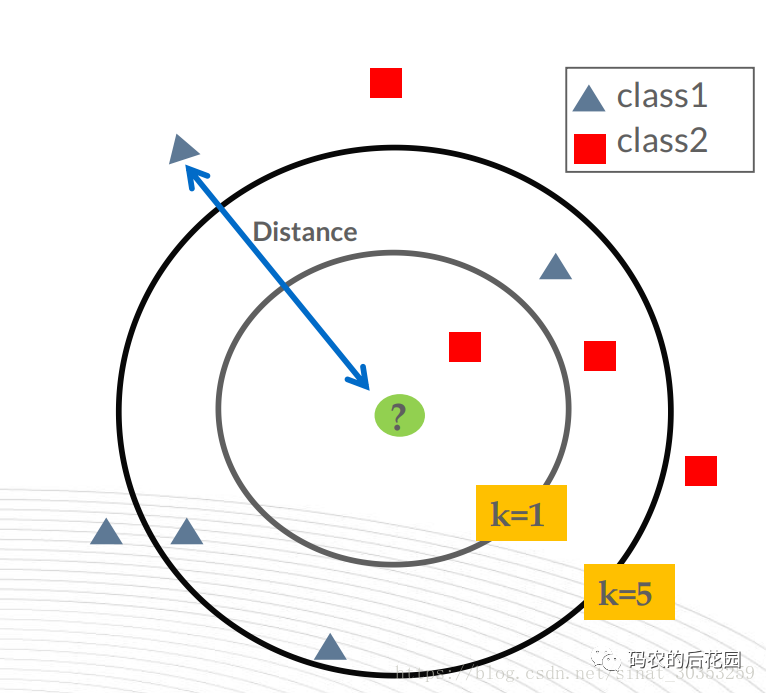
KNN算法的思想是:一个样本A与数据集中的k个样本最相似, 如果这k个样本中的大多数样本都属于某一个类别 i, 则该样本 A也属于这个类别 i。(KNN的原理就是当预测一个新的值x的时候,根据它距离最近的K个点中多数点是属于什么类别来判断x属于哪个类别。)
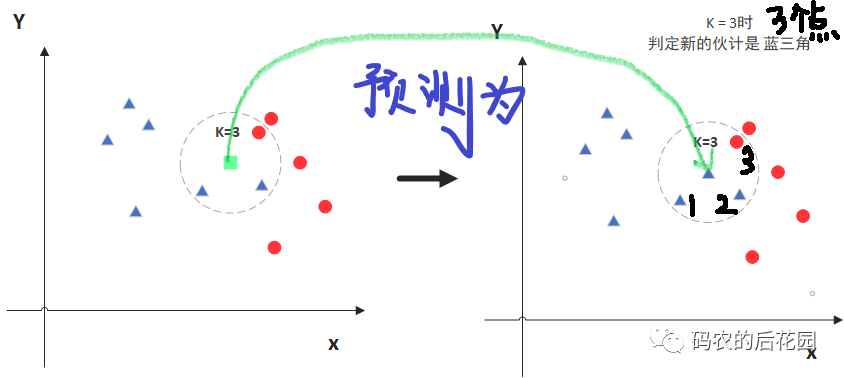
左边的中间绿色的正方形的点是我们添加要预测类别的点,假设选距离该绿色正方形最近的K=3个数据集中已知类别的样本点来预测该绿色正方形点属于什么类别,可以看出距离要预测的绿色点的3个数据集中样本点中属于红色的圆形点多一些,那么该绿色的正方形就归类到蓝三角类别。
但是当K=5时,也就是选取5个距离要预测的绿色的点最近的数据集中的已知类别样本点对其(绿色的点)进行预测类别,如下图,这次距离要预测的绿色点的5个数据集中样本点中属于红色的圆形点多一些,所以将要预测的绿色的正方形点归类为红色圆类别。
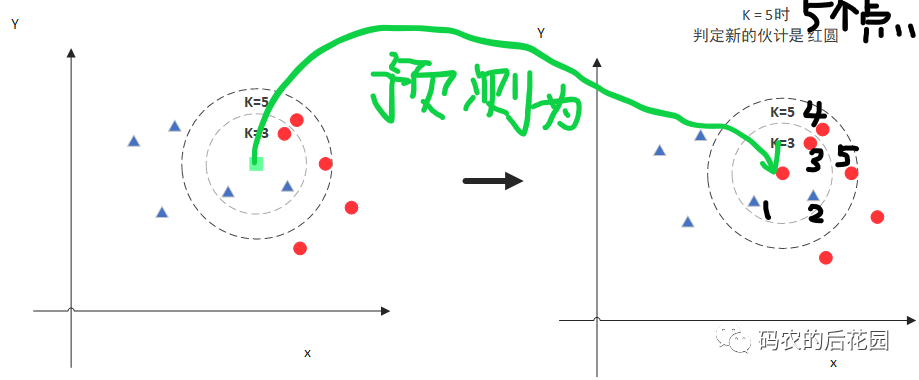
这就是KNN算法的实现原理,可以知道要实现KNN算法,需要进行K值(数据集中已知类别的样本点)选取 和 预测点和数据集中所有已知类别的样本点之间的距离计算,以得到K个距离最近样本点,根据这K个已知类别的样本点中绝大多数什么类别来划分要预测点的类别。
KNN算法实现流程
为了判断未知实例的类别,以所有已知类别的实例作为参照。
1.定义选取参数K
2.计算已知类别数据集中的样本点与当前预测点之间的距离,并按距离递增次序排序
3.选取与预测点距离最近的数据集中K个已知类别的样本点
4.统计距离最近的K个样本点的类别出现的频率
5.将预测点归类为距离最近的K个样本点的类别中出现频率最高的类别
如下,距离新添加紫色点距离最近的7个点中,绿色圆点有4个,所以新加入紫色圆点的类别被判别为绿色圆点的类别。
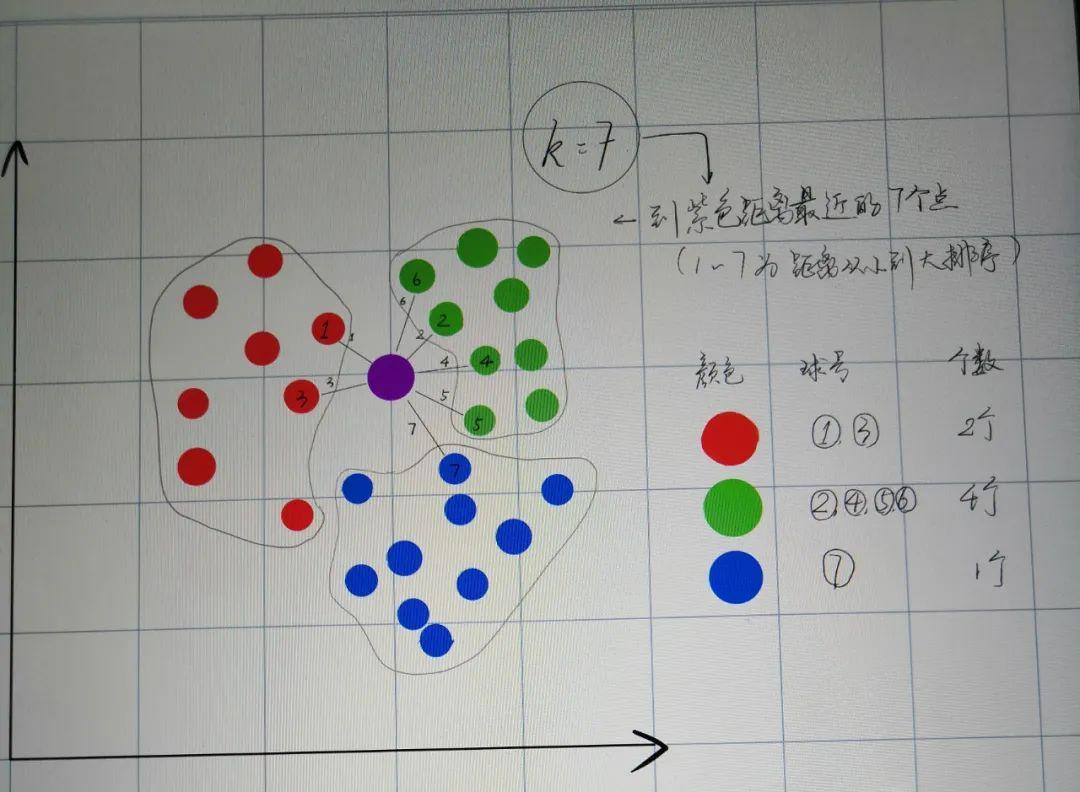
总结:KNN算法主要的点有两个K值的选取和点距离的计算。
K值选取
在应用中,K值一般取一个比较小的数值,通常采用交叉验证法来选取最优的K值,从选取一个较小的K值开始,不断增加K的值,然后计算验证集合的方差,最终找到一个比较合适的K值。
交叉验证法是指将样本数据按照一定比例,拆分出训练用的数据和验证用的数据,比如6:4拆分出部分训练数据和验证数据。
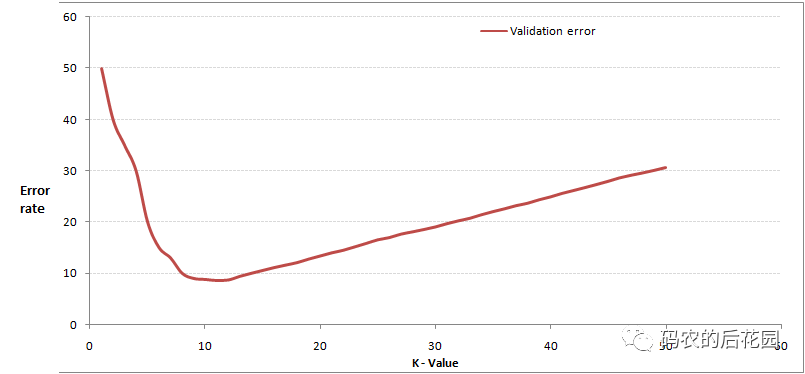
通过交叉验证计算方差得到的图如上,当增大K时,周围有更多的样本可以借鉴,分类效果会变好,错误率会先降低; 但是当K值增大一定的程度时,错误率会变高,举例来说,当你一共35个样本,K值增大到30,KNN算法就没有意义了。
距离度量计算
距离越近,就越相似,属于这一类的可能性就越大,度量空间中的点距离计算的方式分三种类别:L1范数(曼哈顿距离)、L2范数(欧式距离)、切比雪夫距离,KNN算法中使用的欧式距离。
(1)二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离:
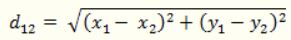
(2)三维空间两点a(x1,y1,z1)与b(x2,y2,z2)间的欧氏距离:
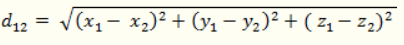
(3)两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离:
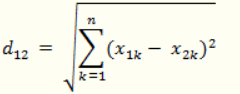
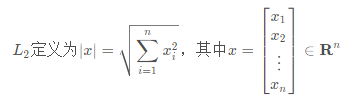
KNN算法最简单粗暴的就是将预测点与数据集中K个已知类别所有样本点距离进行计算,然后保存并排序,选出前面K个值看看哪些类别比较多。
KNN算法代码实例
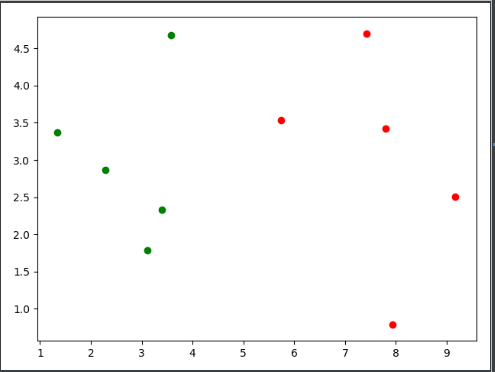
定义训练数据集样本点和样本点所对应的类别,并使用scatter绘制样本点,类别为0的样本点用绿色圆点绘制,类别为1的样本点用红色圆点绘制。
import numpy as np
import matplotlib.pyplot as plt
# 定义训练数据集样本矩阵
raw_data_x = [[3.393533211, 2.331273381],
[3.110073483, 1.781539638],
[1.343808831, 3.368360954],
[3.582294042, 4.679179110],
[2.280362439, 2.866990263],
[7.423436942, 4.696622875],
[5.745051997, 3.533989803],
[9.172168662, 2.511101045],
[7.792783481, 3.424088941],
[7.939820817, 0.791637231]]
#样本点的类别
raw_data_y = [0,0,0,0,0,1,1,1,1,1]
# 将矩阵转换为numpy中的矩阵用于计算
X_train = np.array(raw_data_x)
y_train = np.array(raw_data_y)
# 使用scatter绘制样本点散点图
plt.scatter(X_train[y_train==0,0],X_train[y_train==0,1],color = "g")
plt.scatter(X_train[y_train==1,0],X_train[y_train==1,1],color = "r")
plt.show()
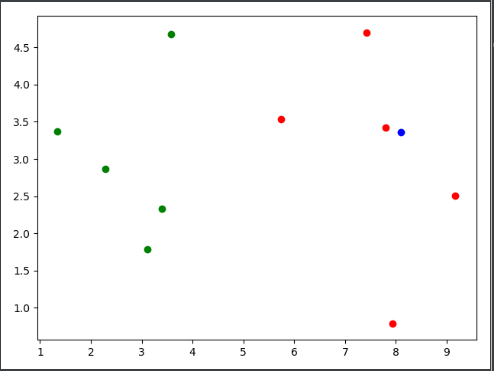
将数据集中的样本点输入到sklearn中KNN算法进行训练,并添加新的数据点蓝色圆点x,定义K=3,即使用训练集中已知类别的3个样本点对蓝色圆点的类别进行预测,使用训练好了的KNN算法进行预测分类,判断新添加的蓝色圆点是类别0还是类别1。
# 使用sklearn中的KNN算法
# 导入KNN算法的库
from sklearn.neighbors import KNeighborsClassifier
# 创建KNN算法对象
KNN_classifier = KNeighborsClassifier(n_neighbors=3)
# 将训练样本点数据添加至KNN算法对象进行训练
KNN_classifier.fit(X_train,y_train)
# 添加一个新的样本点
x = np.array([8.093607318, 3.365731514])
plt.show()
#用训练好的KNN对象预测新数据
y_predict = KNN_classifier.predict(x.reshape(1,-1))
print(y_predict[0]) # 1 属于类别 1
这里可视化可以看到蓝色圆点距离最近的是3个类别为1的红色圆点,所以蓝色圆点的类别应该被预测为1,这里预测成功。
K值的选择,交叉验证
在使用KNN算法之前,我们要先决定K的值是多少,要选出最优的K值,可以使用sklearn中的交叉验证方法。
这里使用鸢尾花数据集,该数据集主要包含了鸢尾花的花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性(特征),以及鸢尾花卉属于『Setosa,Versicolour,Virginica』三个种类中的哪一类。
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
#读取鸢尾花数据集
iris = load_iris()
x = iris.data
y = iris.target
k_range = range(1, 31)
k_error = []
#循环,取k=1到k=31,查看误差效果
for k in k_range:
knn = KNeighborsClassifier(n_neighbors=k)
#cv参数决定数据集划分比例,这里是按照5:1划分训练集和测试集
scores = cross_val_score(knn, x, y, cv=6, scoring='accuracy')
k_error.append(1 - scores.mean())
#画图,x轴为k值,y值为误差值
plt.plot(k_range, k_error)
plt.xlabel('Value of K for KNN')
plt.ylabel('Error')
plt.show()
选出最优的K值,运行结果图:
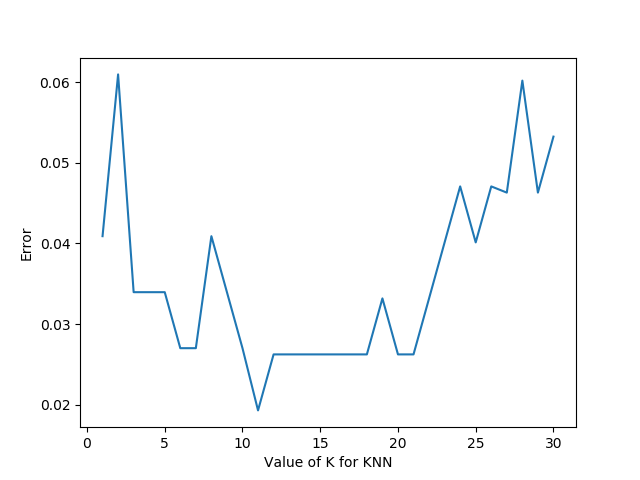
我们就能明显看出K值取多少的时候误差最小,这里明显是K=11最好。当然在实际问题中,如果数据集比较大,那为减少训练时间,K的取值范围可以缩小。
总结
KNN算法原理简洁明了,根据训练数据类型建立模型,模型训练时间快,对异常值不敏感,但是对内存要求高,因为算法存储了所有训练数据,预测阶段可能很慢。
代码完整下载,后台回复:项目实战,下期讲解无监督学习算法Kemans,干货不易,希望大家能够点赞支持


 。
。
参考:
https://www.cnblogs.com/listenfwind/p/10311496.html
https://blog.csdn.net/sinat_30353259/article/details/80901746

分享给更多朋友,转发,点赞,在看