图像分割常见指标 Iou,dice,accuracy,recall,sensitivity,precision,F1-score,specificity 图解以及计算代码
图像分割常见指标计算
指标解释
开始之前需要了解混淆矩阵的知识。另外我还在公式中添加了1e-7作为分子。原因为了避免代码中出现分子为0的情况。本次介绍时,直接写到公式里面。
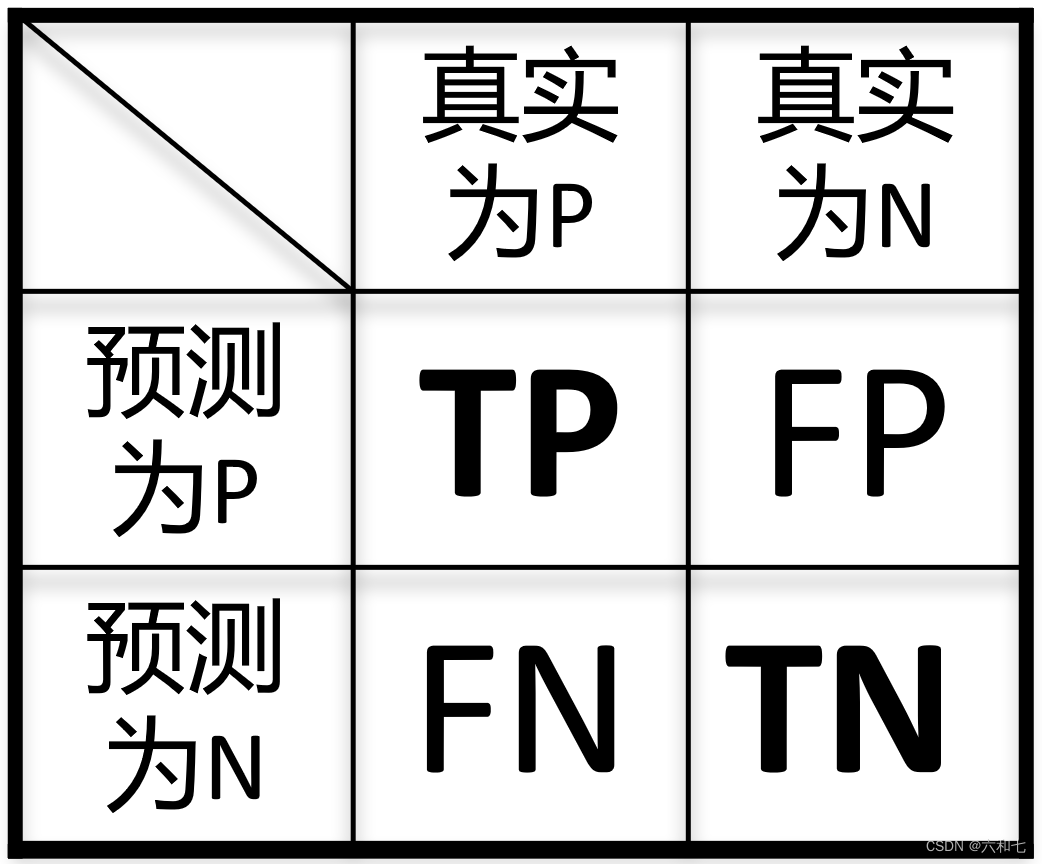
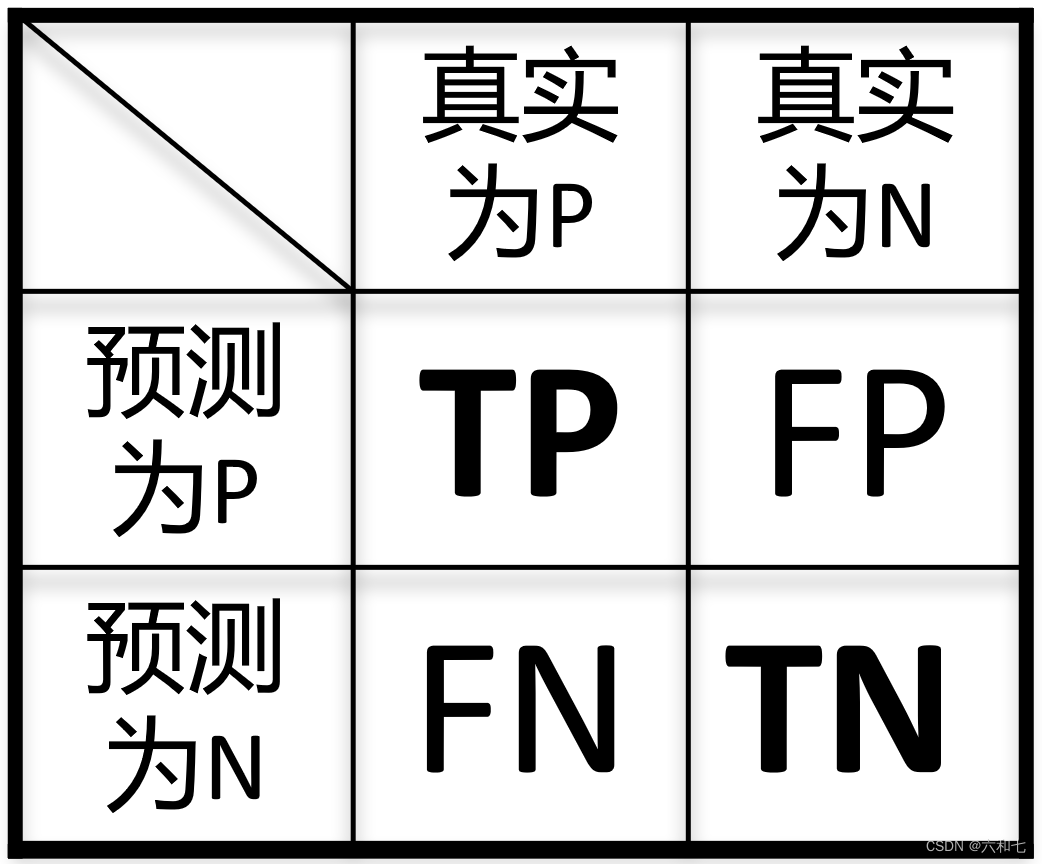
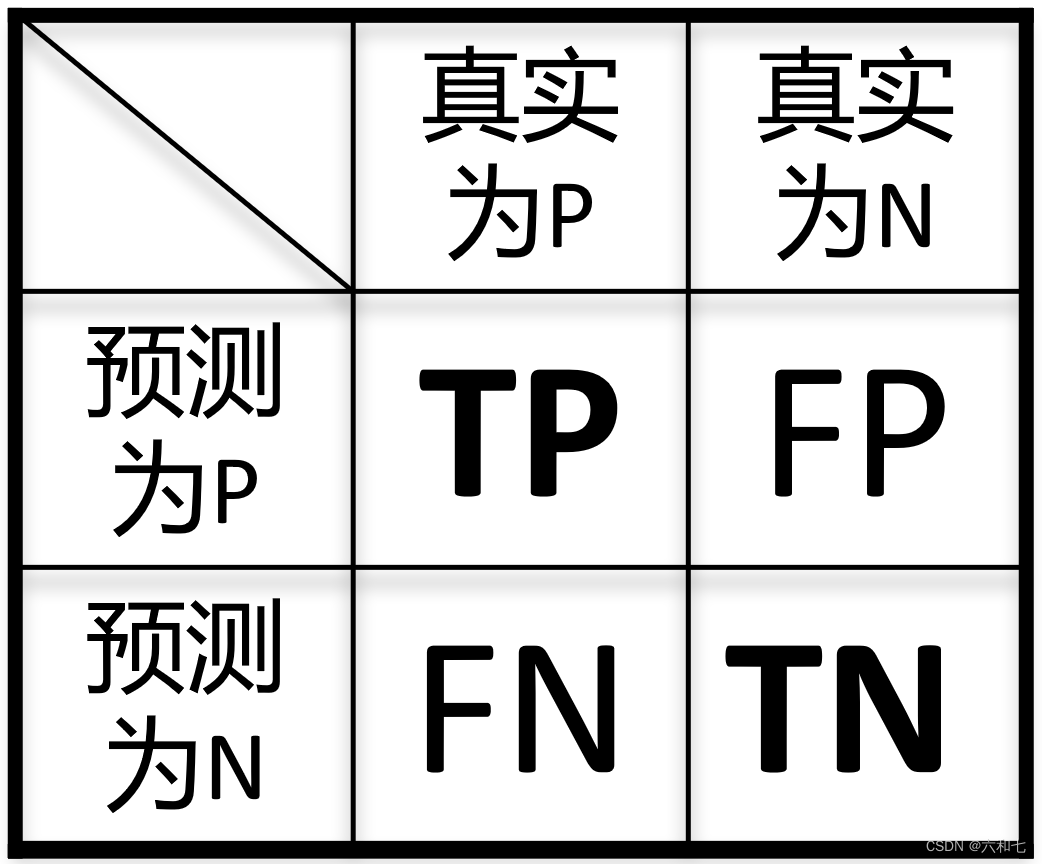
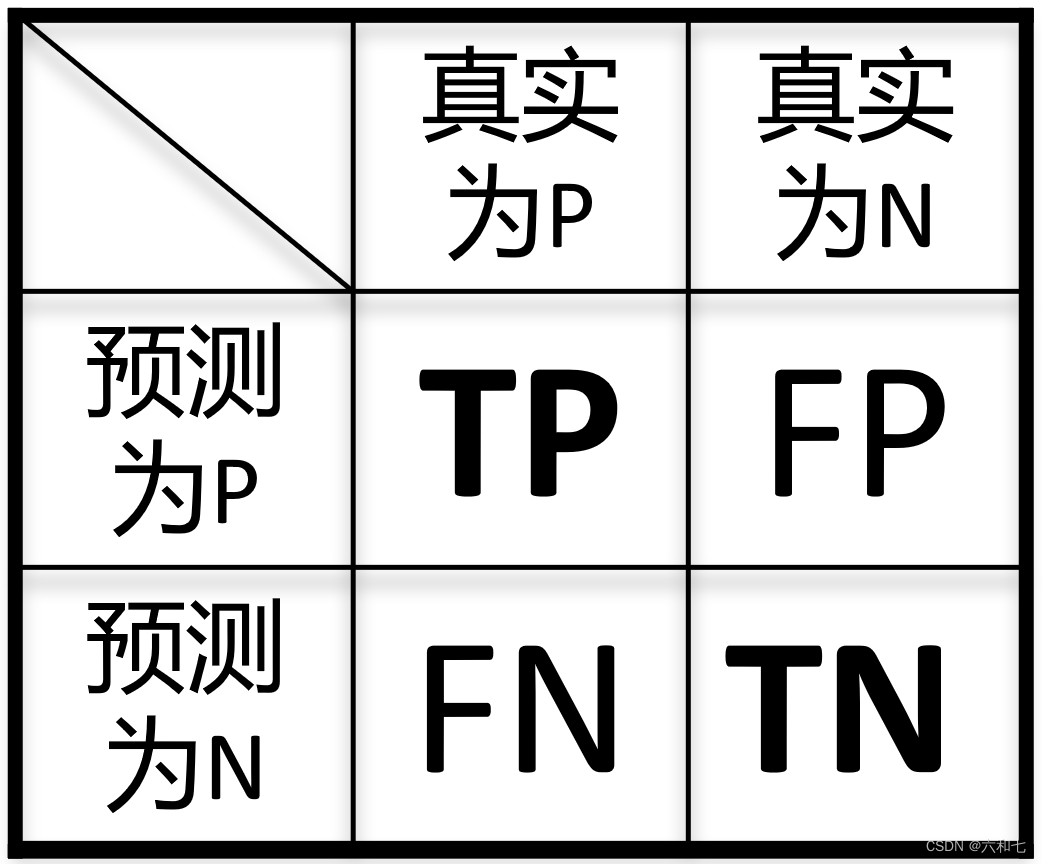
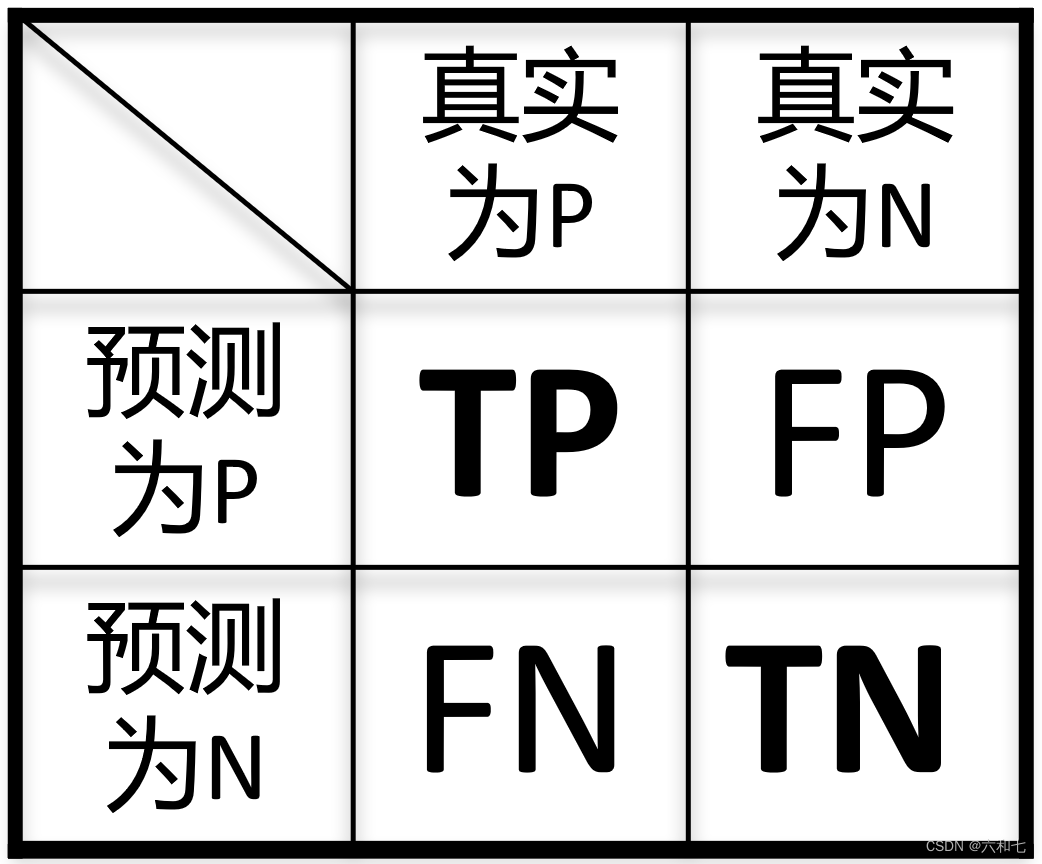
混淆矩阵如图,如何看呢?在进行图像分割时
比如某个像素点,我们预测为类别P ,真实情况是类别P。那么这个像素点的情况就是“一个预测正确的P”,记为TP (True Positive)
比如某个像素点,我们预测为类别P ,真实情况是类别N。那么这个像素点的情况就是“一个预测错误的P”,记为FP (False Positive)
其他(FN,TN)同理。
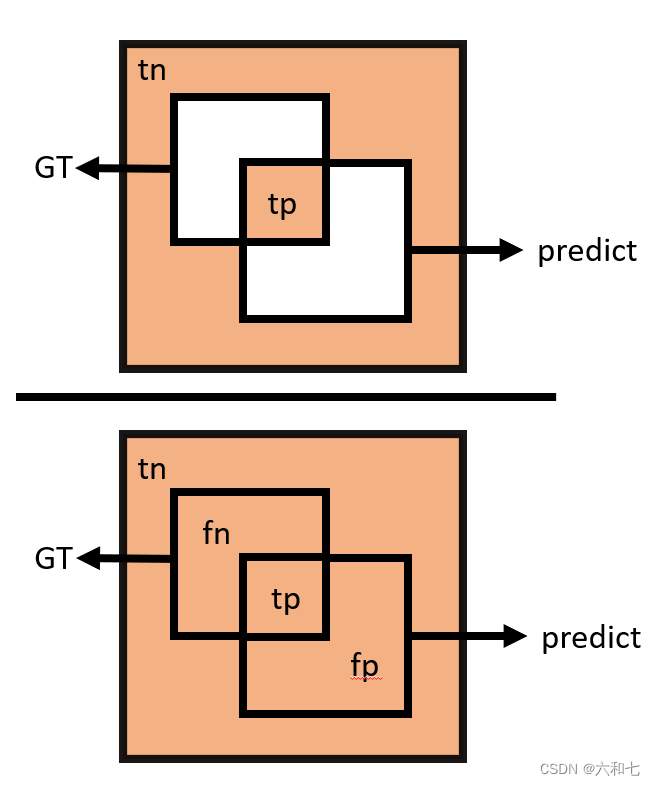
将混淆矩阵放到真实图像中,就是这样的情况。
如图是一张图片的情况,GT就是我们数据集图片标注的区域,predict就是我们模型预测出的区域。
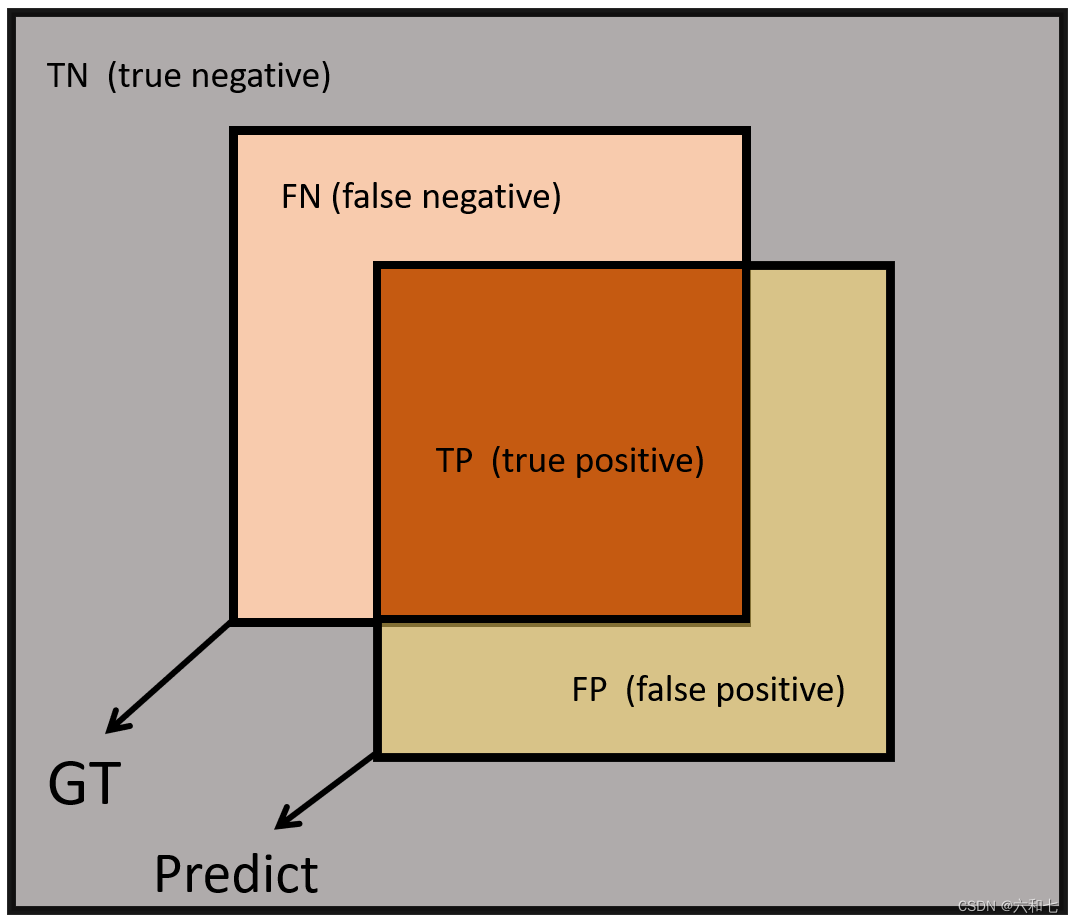
predict与GT一定存在差异,这些差异需要依靠评价指标来衡量。不同的评价指标对不同方向的差异有不同侧重点。
下面介绍评价指标:
IOU,Jaccard index
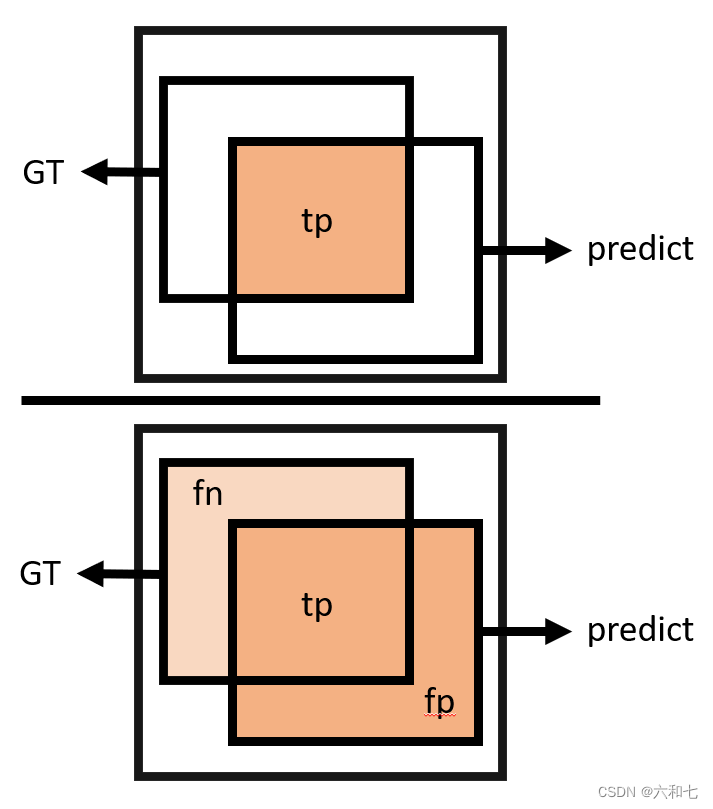
IOU(Intersection over Union)即交并比,顾名思义,即交集与并集的比值。在图像分割中,我们就计算 GT,Predict的交集与并集的比值。
很多论文还会说的杰卡德指数(Jaccard index),其实就是交并比。
| 混淆矩阵 | 公式 | 公式图解 |
|---|---|---|
|
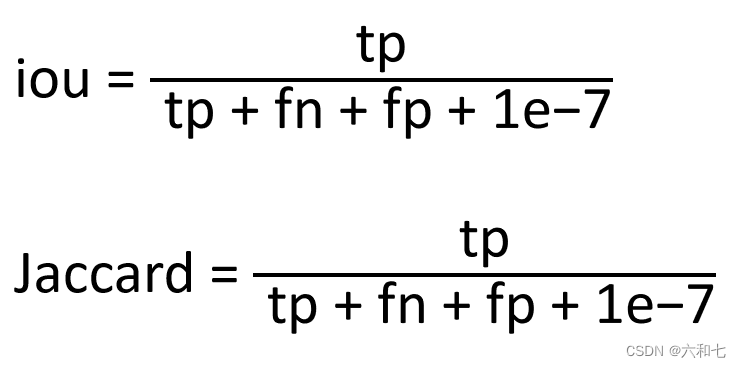
|
|
Dice coefficient,F1-score
网上有很多关于这两个指标的计算,其实就是同一个计算(不服请推导)。
F1-score是为了能够评价不同算法的优劣,在Precision和Recall的基础上提出了F1值的概念,来对Precision和Recall进行整体评价。F1-score(均衡平均数)是综合考虑了模型查准率和查全率的计算结果,取值更偏向于取值较小的那个指标。F1的定义如下:
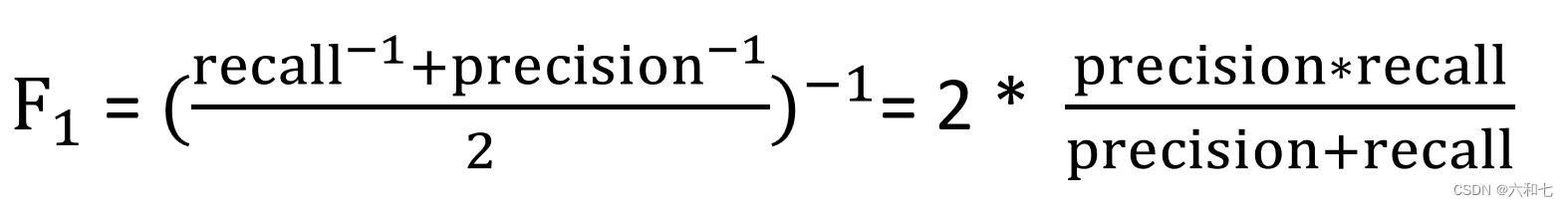
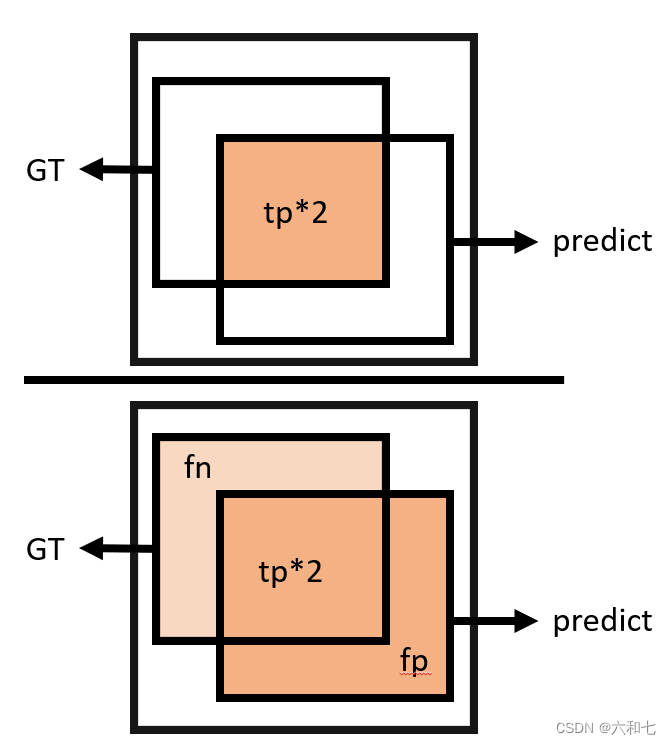
Dice 系数,也称为 F1 分数,是两个集合之间重叠的度量,范围为 0 到 1。值为 1 表示完全重叠,而 0 表示没有重叠。
dice损失,和dice系数(dice coefficient)的关系是:dice loss = 1-dice coefficient。
这个指标很常见,用的频次比 IOU 还多,主要有:
-
Dice 系数广泛用于评估图像分割模型的性能,因此使用 Dice 损失有助于优化该指标的模型
-
Dice 损失可以处理类别不平衡,这通常是医学图像分割中的一个问题,其中某些类别可能比其他类别更普遍。
-
Dice 损失是可微的,这使得它可以与基于梯度的优化算法结合使用。
| 混淆矩阵 | 公式 | 公式图解 |
|---|---|---|
|

|
|
Accuracy
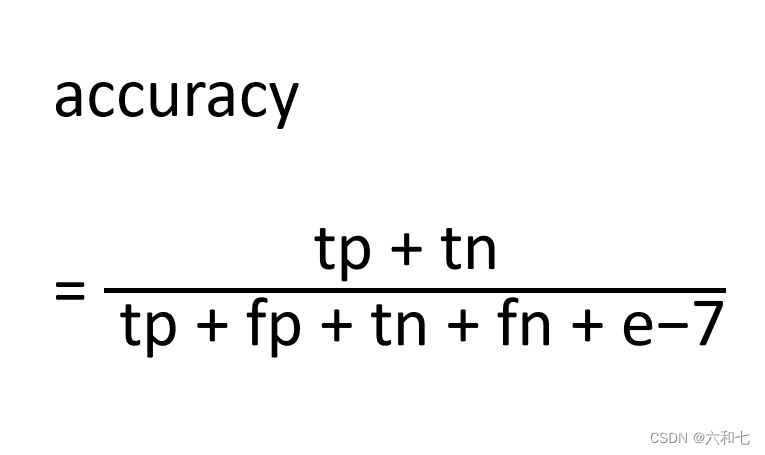
accuracy指的是正确预测的样本数占总预测样本数的比值,它不考虑预测的样本是正例还是负例。如果在代码中只考虑正样本,可以在公式中去掉分子tn。
| 混淆矩阵 | 公式 | 公式图解 |
|---|---|---|
|
|
|
Precision
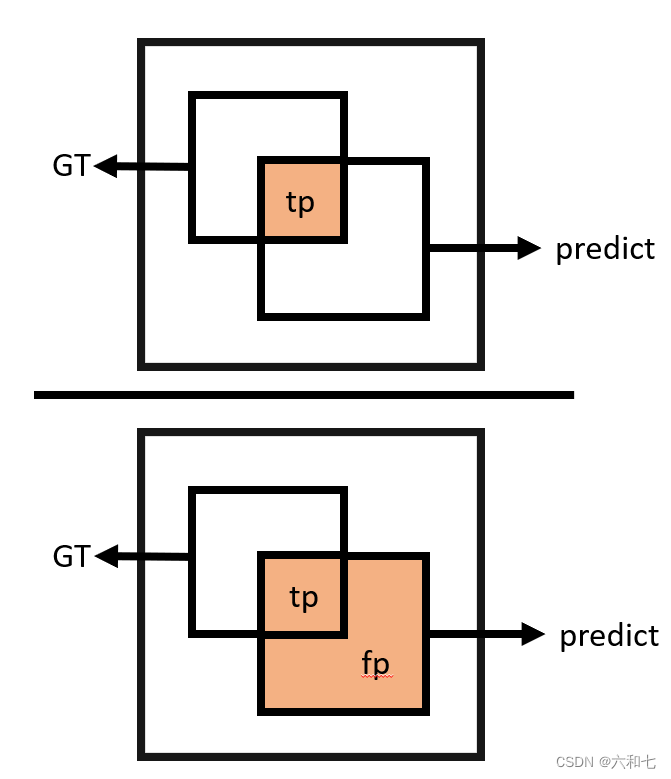
precision指的是所有预测为正样本数中正确预测的正样本数占的比值。
| 混淆矩阵 | 公式 | 公式图解 |
|---|---|---|
|

|
|
Recall,Sensitivity
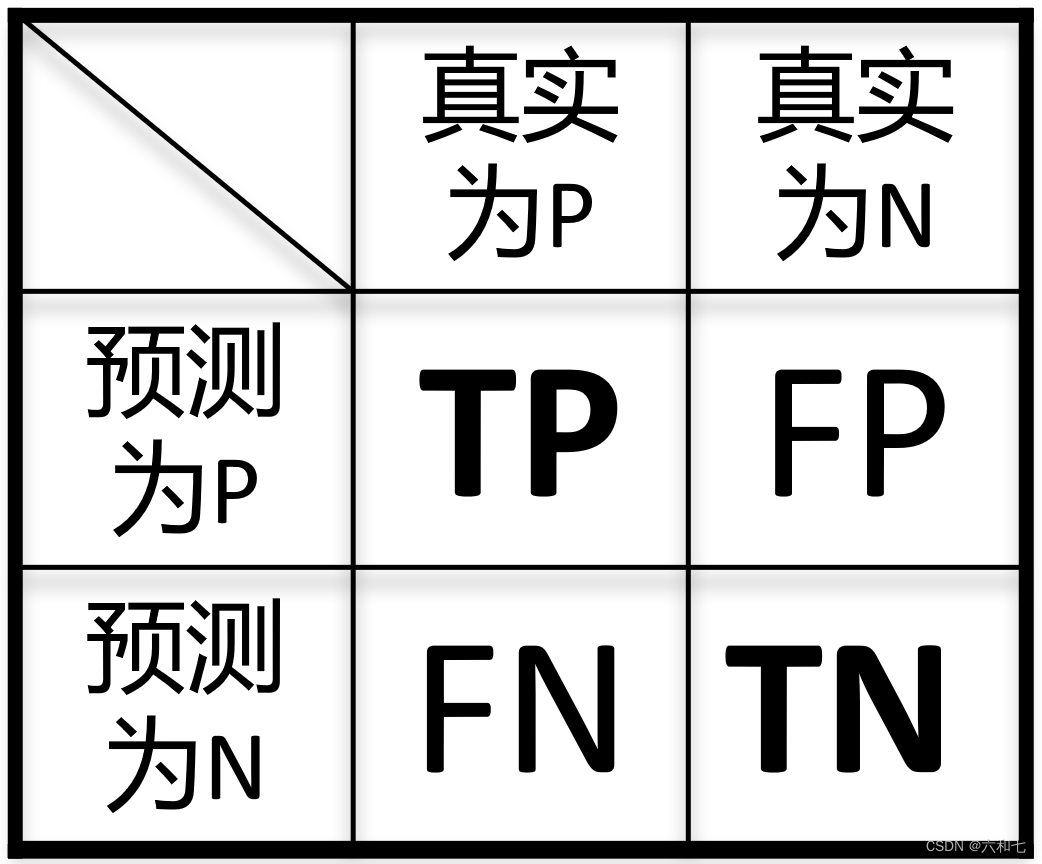
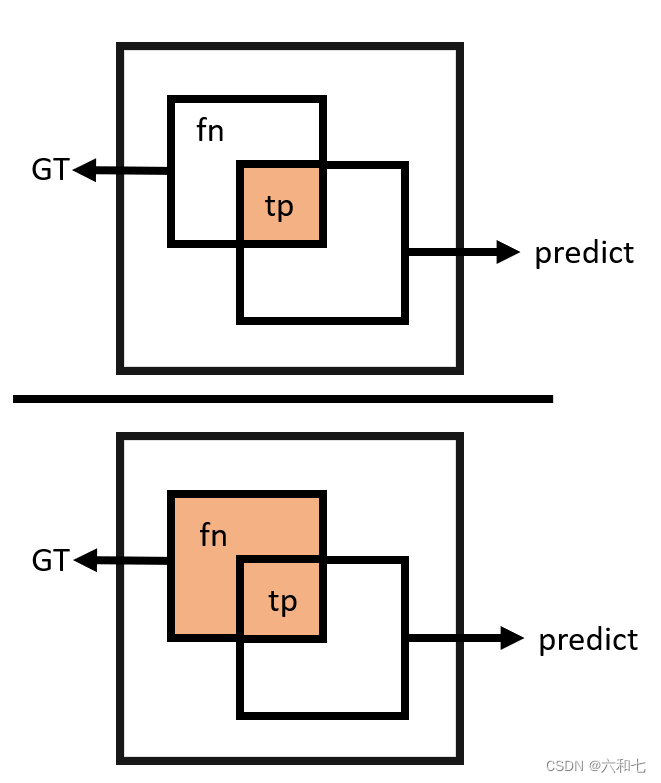
recall又叫召回率,指的是正确预测的正样本数占真实正样本总数的比值。Sensitivity,我们常说“敏感性”,sensitivity的值越大,说明“有病的被判断为有病的”越大,“漏检”(FN)越小。这两个指标公式是一致的。
| 混淆矩阵 | 公式 | 公式图解 |
|---|---|---|
|
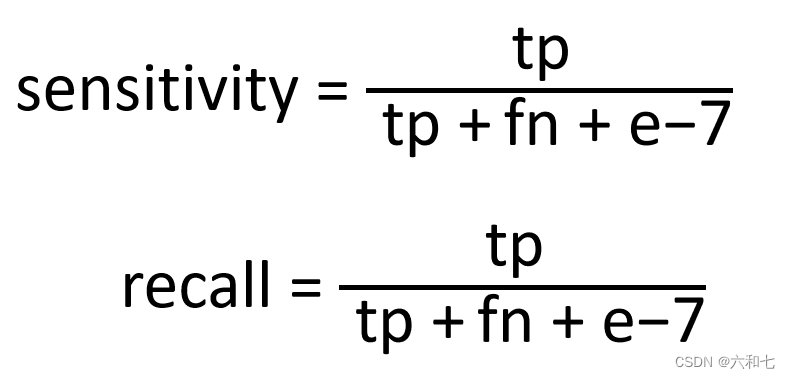
|
|
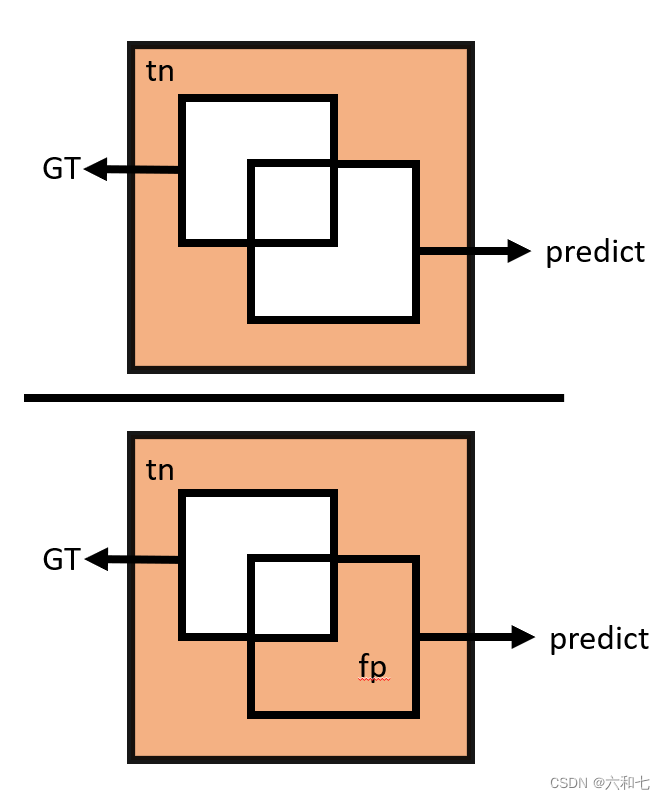
Specificity
Specificity,我们常说“特异性”,Specificity的值越大,说明“健康的被判断为健康的”的越大,“误检”(FP)越小。也叫TNR(True negative rate)
敏感性高=漏诊率低
特异性低=误诊率高
| 混淆矩阵 | 公式 | 公式图解 |
|---|---|---|
|
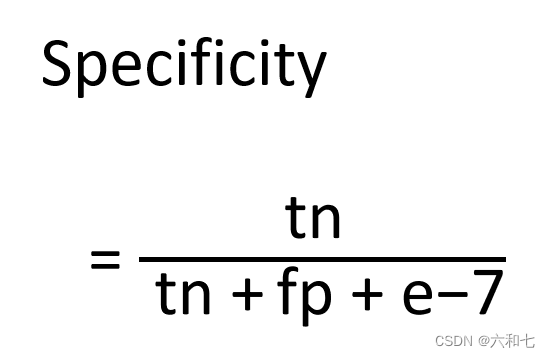
|
|
代码计算
这里代码输入为prediction,gt_image。
prediction代表预测结果,其为值0,255的单通道numpy数组。
gt_image代表真实标注,其为值0,255的单通道numpy数组。
import numpy as np
import cv2
# 输入(单通道预测图,单通道预测图,评价类型)
# 注意,预测图与原图保持,通道,大小一致
# 参考参数(字符串):iou,dice_coefficient,accuracy,precision,recall,sensitivity,f1,specificity
def calculate_metrics(predict_image, gt_image, evaluate):
# 将图像转换为二进制数组
predict_image = np.array(predict_image, dtype=bool)
gt_image = np.array(gt_image, dtype=bool)
# 计算True Positive(TP)
tp = np.sum(np.logical_and(predict_image, gt_image))
# 计算True Negative(TN)
tn = np.sum(np.logical_and(np.logical_not(predict_image), np.logical_not(gt_image)))
# 计算False Positive(FP)
fp = np.sum(np.logical_and(predict_image, np.logical_not(gt_image)))
# 计算False Negative(FN)
fn = np.sum(np.logical_and(np.logical_not(predict_image), gt_image))
# 计算IOU(Intersection over Union)
iou = tp / (tp + fn + fp + 1e-7)
# 计算Dice Coefficient(Dice系数)
dice_coefficient = 2 * tp / (2 * tp + fn + fp + 1e-7)
# 计算Accuracy(准确率)
accuracy = (tp + tn) / (tp + fp + tn + fn + 1e-7)
# 计算precision(精确率)
precision = tp / (tp + fp + 1e-7)
# 计算recall(召回率)
recall = tp / (tp + fn + 1e-7)
# 计算Sensitivity(敏感度)
sensitivity = tp / (tp + fn + 1e-7)
# 计算F1-score
f1 = 2*(precision*recall)/(precision+recall + 1e-7)
# 计算Specificity(特异度)
specificity = tn / (tn + fp + 1e-7)
if evaluate == "iou":
return iou
if evaluate == "dice_coefficient":
return dice_coefficient
if evaluate == "accuracy":
return accuracy
if evaluate == "precision":
return precision
if evaluate == "recall":
return recall
if evaluate == "sensitivity":
return sensitivity
if evaluate == "f1":
return f1
if evaluate == "specificity":
return specificity
使用方式:
import numpy as np
import cv2
predict_image = cv2.imread("./predict/186.jpg", 0)
gt_image = cv2.imread("./gt/186.png", 0)
evaluate = calculate_metrics(predict_image, gt_image, "specificity")
print(evaluate)
evaluate = calculate_metrics(predict_image, gt_image, "f1")
print(evaluate)