Leetcode 题组 26（二叉树）

222. 完全二叉树的节点个数

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

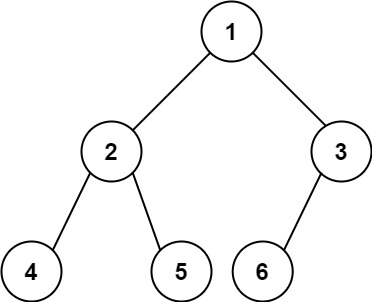
输入：root = [1,2,3,4,5,6]
输出：6

分析：

这个题按照正常递归或者层序遍历都可以写，不过因为是完全二叉树，因此可以使用完全二叉树的性值：满二叉树的节点个数为2^N-1，其中N表示层数（root节点为第1层）。

 我们可以判断当前节点是否为满二叉树，如果是，就可以返回从这个节点到下面所有节点的个数，如果不是，就需要递归的寻找左子树个数和右子树个数。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        // 递归边界
        if (!root) return 0;
        // 判断该节点到下面所有节点是否能构成满二叉树
        TreeNode* left = root->left;
        TreeNode* right = root->right;
        int l_cot = 0, r_cot = 0;
        while(left) {
            left = left->left;
            ++l_cot;
        }
        while(right) {
            right = right->right;
            ++r_cot;
        }
        // 如果能构成满二叉树 返回 2^N-1
        if (l_cot==r_cot) {return pow(2,l_cot+1) - 1;}
        // 否则需要递归的寻找左子树和右子树的个数
        else return countNodes(root->left)+countNodes(root->right)+1;
    }
};

110. 平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

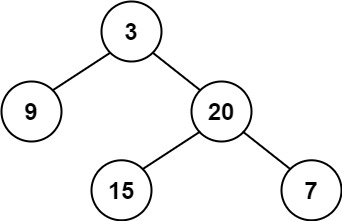
输入：root = [3,9,20,null,null,15,7]
输出：true

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:

    int deep(TreeNode* node){
        if (!node) return 0;
        else return max(deep(node->left), deep(node->right))+1;
    }

    bool isBalanced(TreeNode* root) {
        if (!root) return true;
        int l_cot = deep(root->left);
        int r_cot = deep(root->right);
        return abs(l_cot-r_cot)<=1 && isBalanced(root->left) && isBalanced(root->right);
    }
};

 257. 二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。
示例 1：

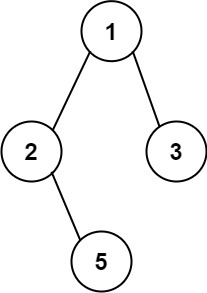
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:

    void dfs(TreeNode* node, vector<string>& ans, string path){
        path = path + "->" + to_string(node->val);
        if (!node->left&&!node->right) {
            ans.push_back(path);
            return;
        }
        if (node->left) dfs(node->left, ans, path);
        if (node->right) dfs(node->right, ans, path);
    }

    vector<string> binaryTreePaths(TreeNode* root) {
        if (!root) return {};  
        if (!root->left&&!root->right) return {to_string(root->val)};
        vector<string> ans;
        if (root->left) dfs(root->left, ans, to_string(root->val));
        if (root->right) dfs(root->right, ans, to_string(root->val));
        return ans;
    }
};