深度学习_CNN
CNN反向推导链式法则

链式法则求导示例
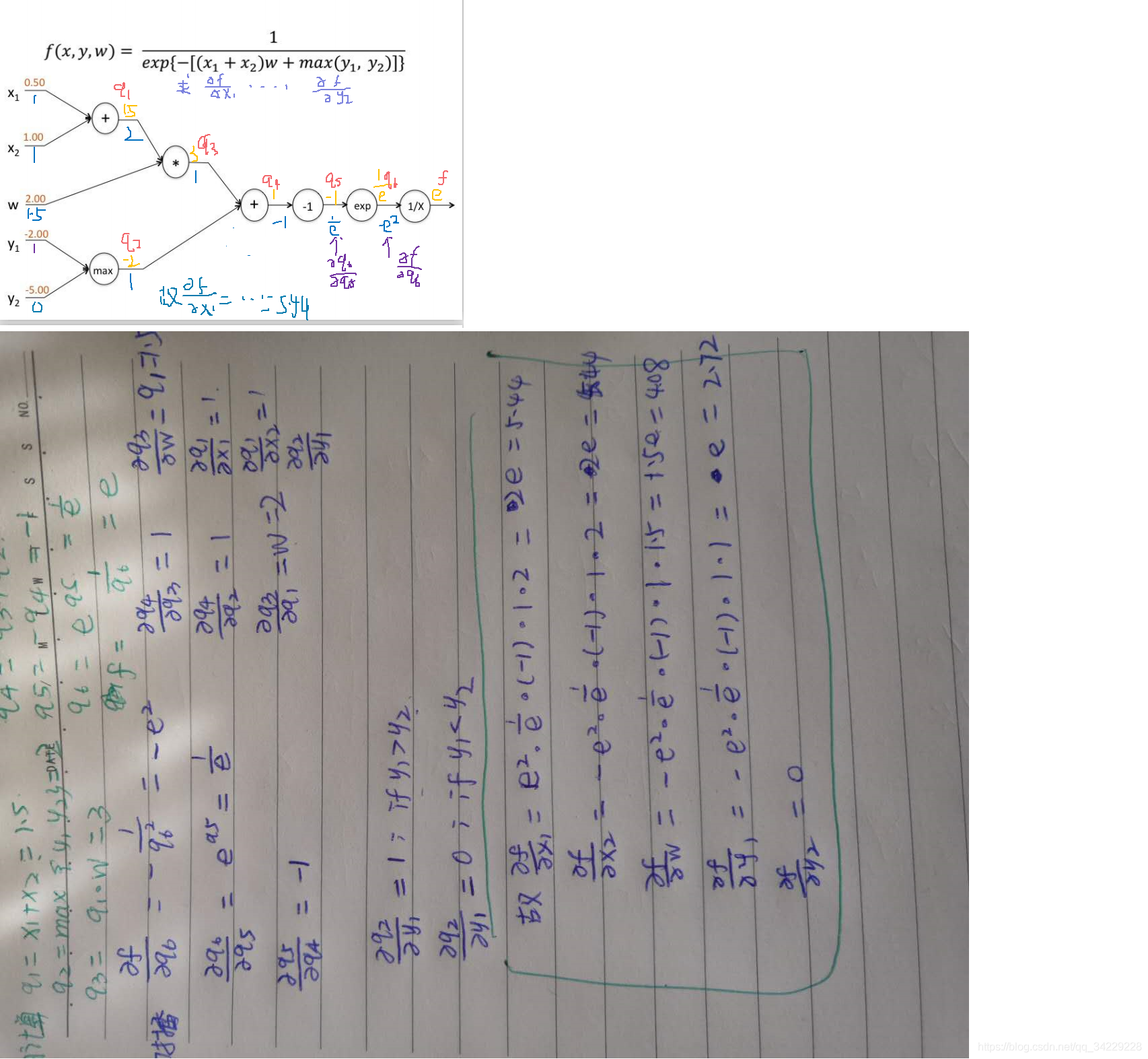
卷积神经网络也是这样一层一层从后到前传递梯度的,有了梯度后,就可以更新参数。上图中max模拟了池化过程,此时部分神经元失活。
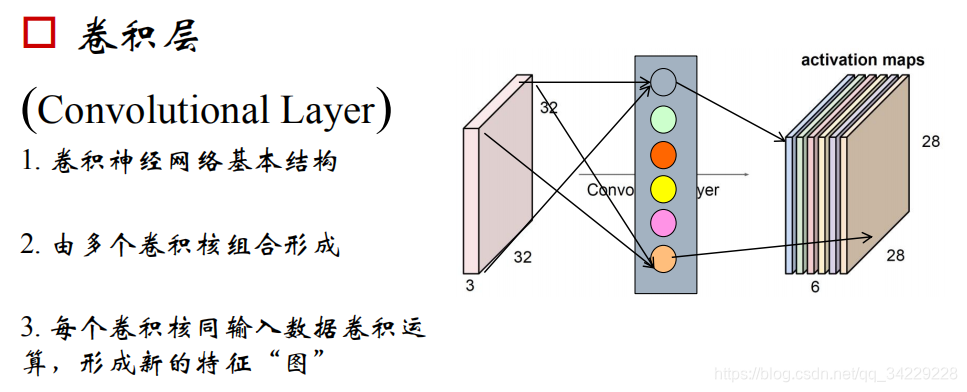
CNN—卷积层
注意:原图片每个pixel可以看作神经网络的输入,权值则是对应的卷积层的每一个值。故最后需要训练的参数为卷积层的值和神经网络的阈值。
我们通常会使用多层卷积层来得到更深层次的特征图。卷积层主要进行的操作是对图片进行特征提取,随着卷积层的深入它提取到的特征就越高级。如下:
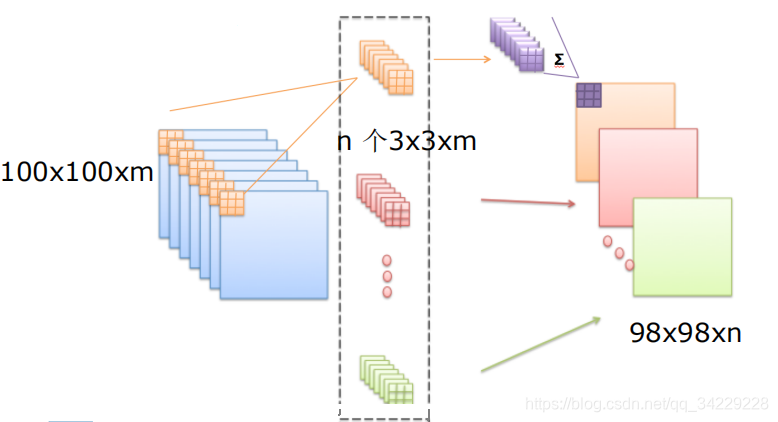
上图有6个5*5*3的卷积核,对应输出的激励特征图为28*28*6的。即对应输出的神经元有28*28*6个。对于任意一个神经元,它对应的连接为5*5*3;故每个神经元有75个权值。
神经元权值共享原则
卷积神经网络引入“权值”共享原则,即一个特征图上每个神经元对应的75个权值参数被每个神经元共享,这样6个核总共需要75*6个权值参数,而每个特征图的阈值也共享,即需要6个阈值,则总共需要75*6+6个参数。
注意若卷积层为3*3*3的则,上图卷积输出为30*30*1,因为边缘不作为卷积核中心计算。n个卷积核产生n个输出(n个激励特征图)(如下图)。
卷积核基本概念:
- 同输入数据进行计算的二维(一维,三维)算子
- 大小(size)用户定义,深度输入数据定义
大小一般为奇数,深度与原始数据深度相同 - 卷积核“矩阵”值:卷积神经网络的参数
- 卷积核初值随机生成,通过反向传播更新
卷积核参数
- 步长
- 卷积核大小
- 边界扩充(确保卷积后特征图尺度一致)(扩充方法:卷积核的宽度2i+1,
添加pad宽度为i) - 卷积核数目(64、128、256 Why:GPU并行更高效)
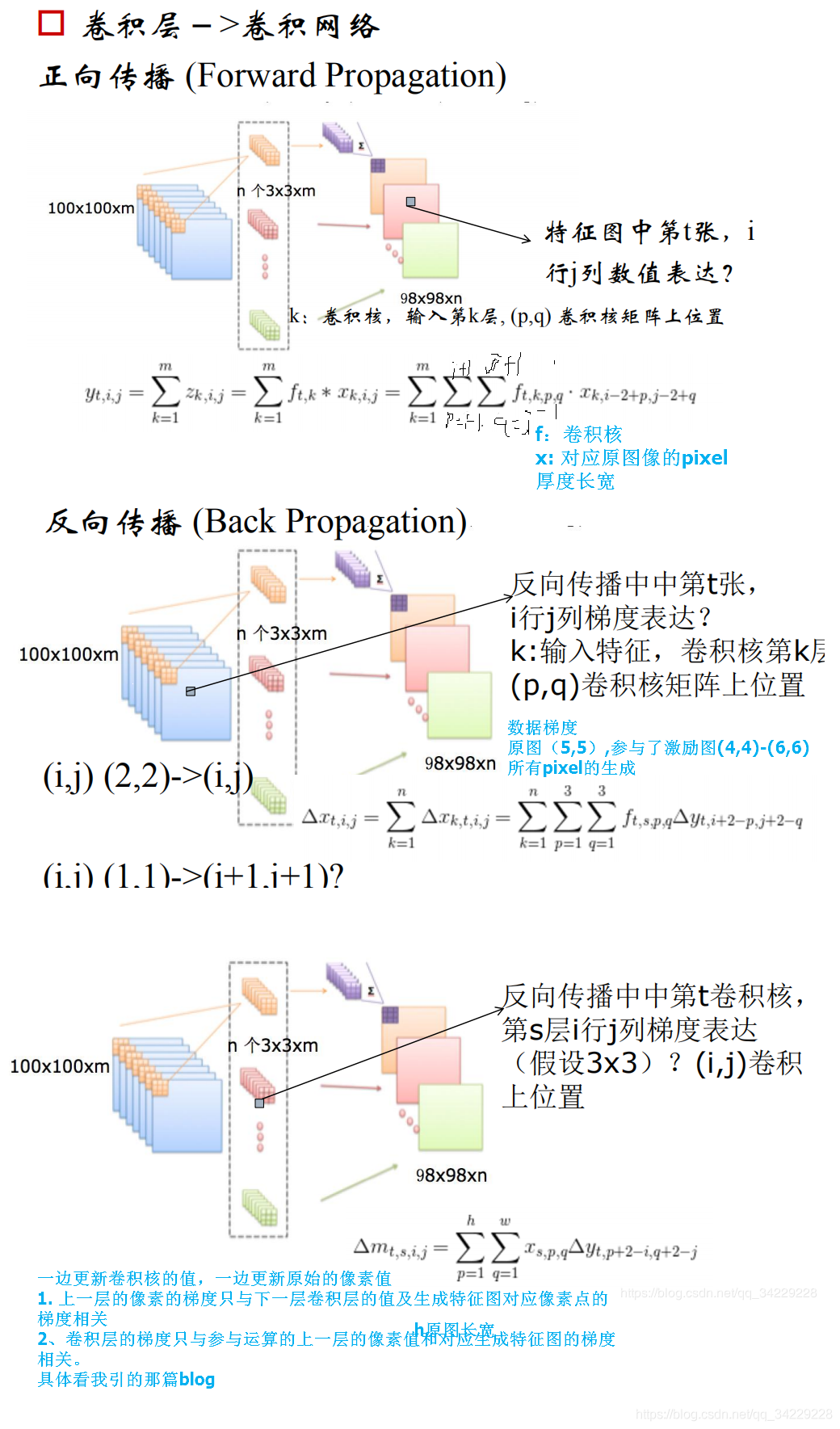
CNN正向传播,反向计算
CNN正向传播和反向传播的推导
CNN_功能层
- Relu:卷积是线性运算,增加非线性描述能力
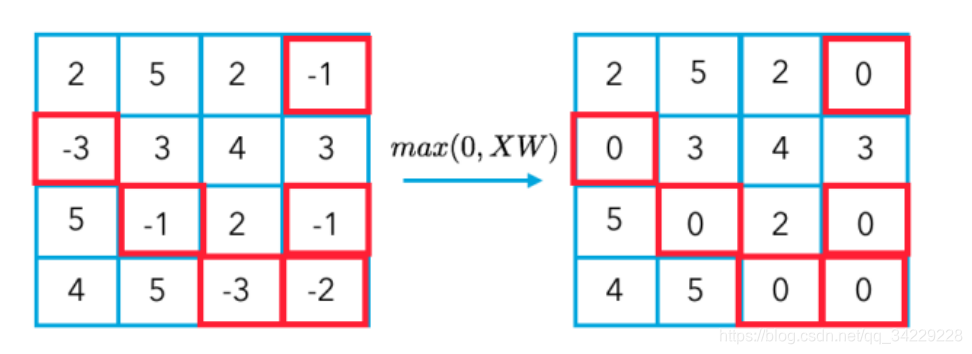
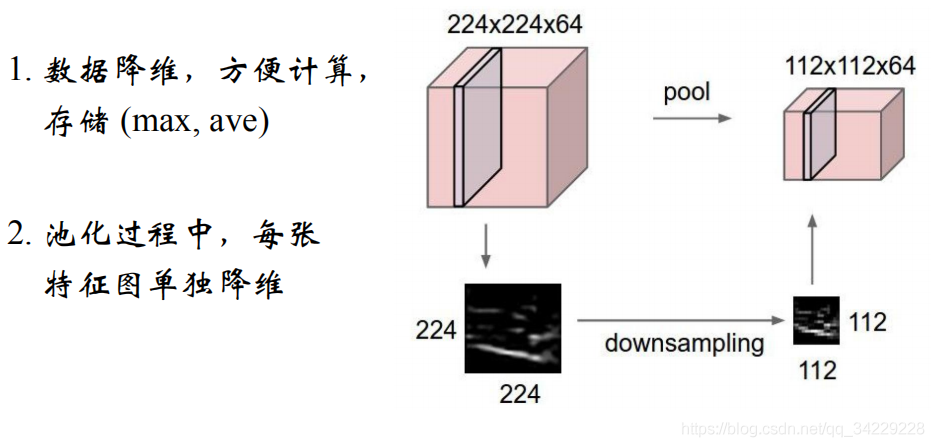
- Pooling:降维,使特征图稀疏,减少数据运算量,保持精度
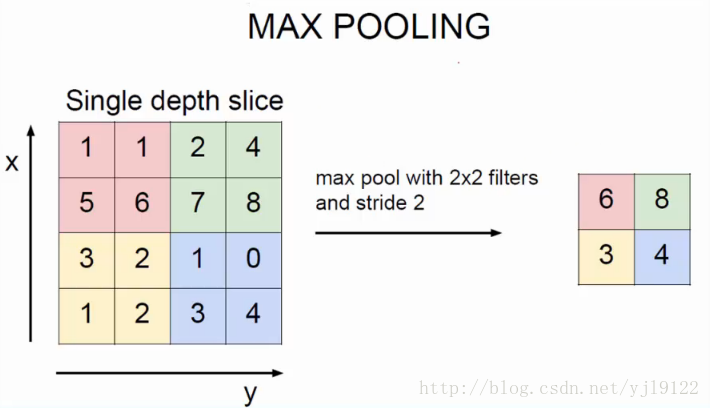
池化操作具体实现,以最大值池化为例。(将图片按卷积核大小均匀分块,对每一块区域选取最大值,以下图为例)
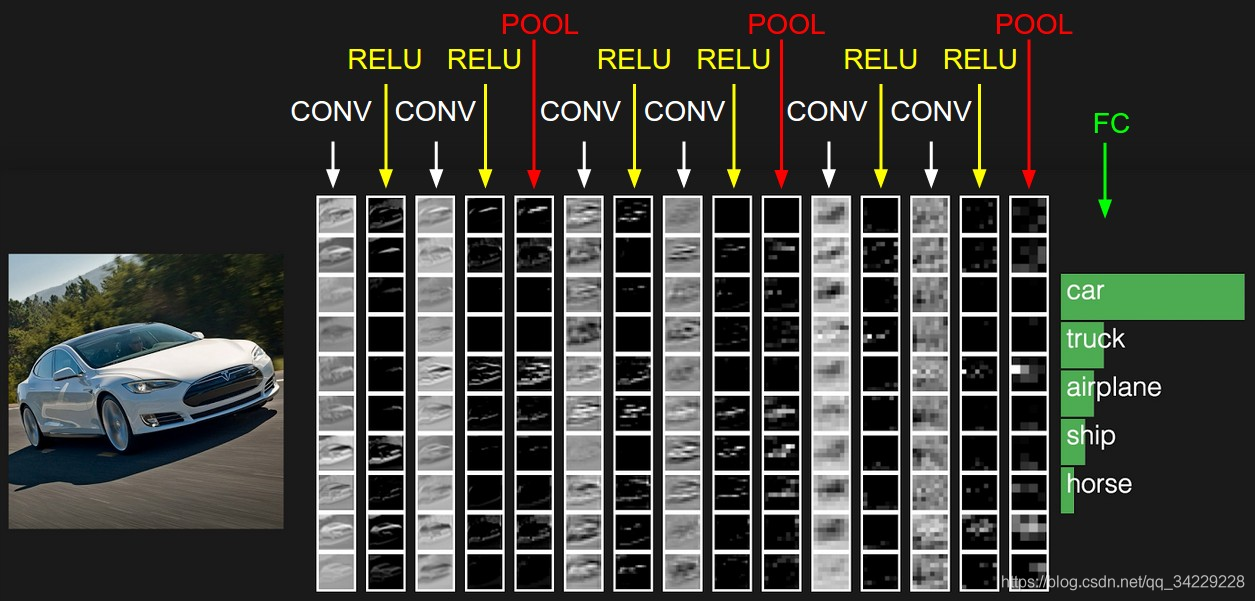
小小结
CNN=卷积层+Relu+池化+…+全连接层
-
归一化层:特征的scale保持一致

-
切分层:不同区域进行独立学习
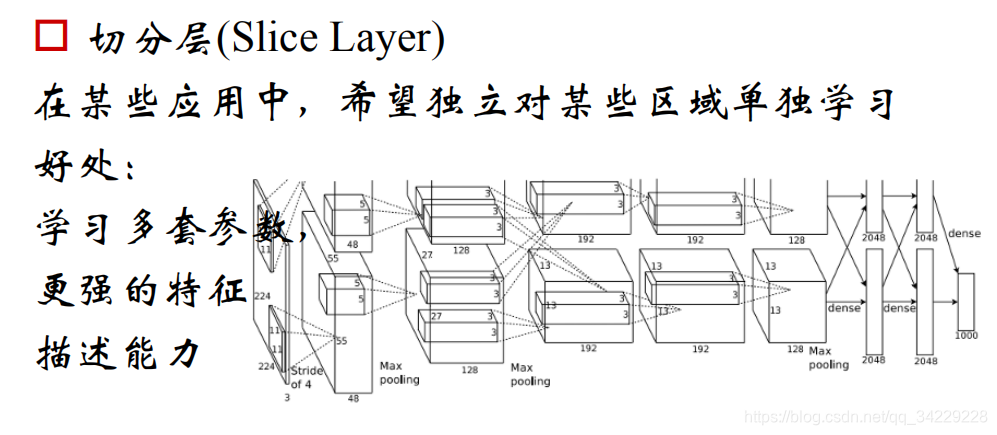
-
融合层:对分开的区域合并,方便信息融合
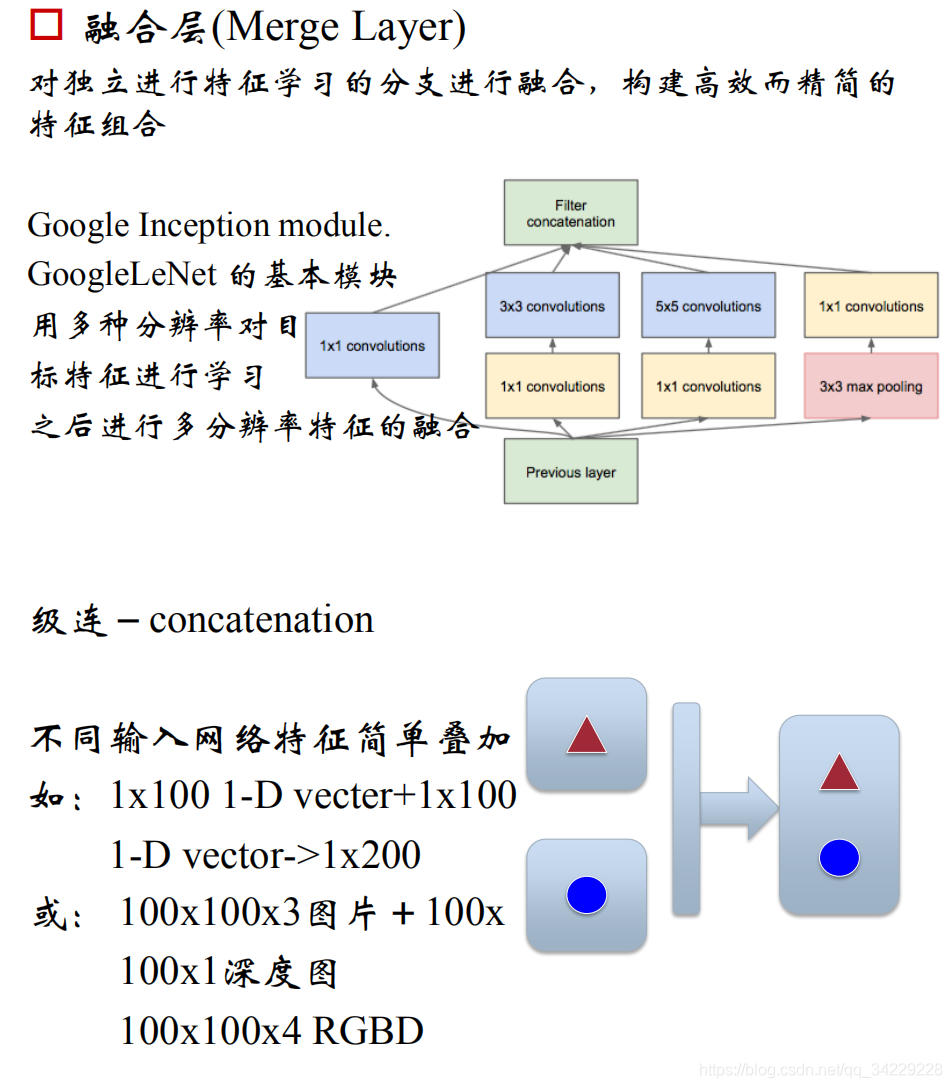
-
增加图片生成或探测任务中空间信息
卷积神经网络与传统神经网络相比优点?
传统的全连接神经网络,下一层与上一层的所有神经元都有连接,训练参数多;二添加卷积层后,下一层只与卷积区域神经元相关。如下图
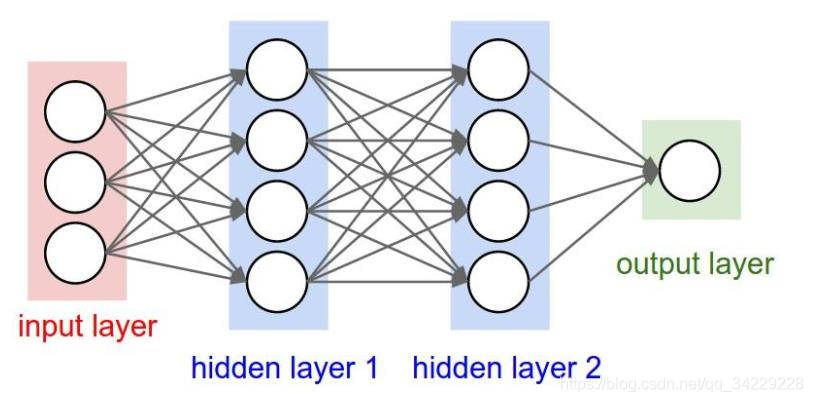
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NRDV4At7-1586779723070)(http://ufldl.stanford.edu/wiki/images/thumb/9/99/Network331.png/400px-Network331.png#pic_center)]](https://images2.imgbox.com/1e/fc/ccMnHRvK_o.png)
CNN优缺点
