计算机视觉——基础矩阵

一、外极几何原理

为了解释基础矩阵，我们要先了解一下外极几何的相关知识。
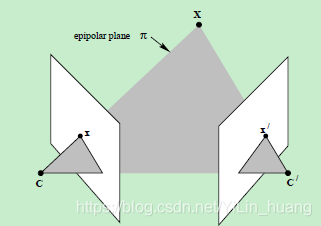
提到对极几何，一定是对二幅图像而言，对极几何实际上是“两幅图像之间的对极几何”，它是图像平面与以基线为轴的平面束的交的几何（这里的基线是指连接摄像机中心的直线），以下图为例：对极几何描述的是左右两幅图像(点x和x’对应的图像)与以CC’为轴的平面束的交的几何！

八点估算法

基本矩阵是由该方程定义的
$$X^{\prime T}Fx=0$$
其中x↔x′是两幅图像的任意一对匹配点。由于每一组点的匹配提供了计算F系数的一个线性方程，当给定至少7个点（3×3的齐次矩阵减去一个尺度，以及一个秩为2的约束），方程就可以计算出未知的F。我们记点的坐标为x=(x,y,1)T，x′=(x′,y′,1)T
又F为：

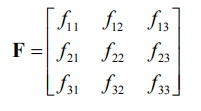
则：

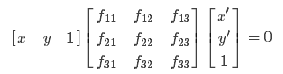
即相应方程式为

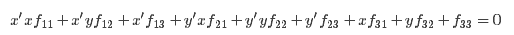
求解上面的方程组就可以得到基础矩阵各个元素了。当然这只是理想中的情况，由于噪声、数值的舍入误差和错误的匹配点的影响，仅仅求解上面的线性方程组得到的基础矩阵非常的不稳定，在实际计算中，可以直接用ATA的分解来求解参数。也可以用非线性优化，通过搜索f使得||Af||最小化,同时满足||f||=1的约束，上述求解后的F不一定能满足秩为2的约束，因此还要在F基础上加以约束。
通过SVD分解可以解决，令F=UΣVT，又因为要秩为2，所以这里取最后一个元素设置为0，则

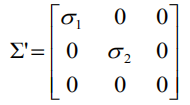
二、实验分析

实验源码：

# coding: utf-8
from PIL import Image
from numpy import *
from pylab import *
import numpy as np
from PCV.geometry import homography, camera, sfm
from PCV.localdescriptors import sift

camera = reload(camera)
homography = reload(homography)
sfm = reload(sfm)
sift = reload(sift)

# 提取特征
im1 = array(Image.open('C:/Users/13799/PycharmProjects/untitled1/pic1/20.jpg'))
sift.process_image('C:/Users/13799/PycharmProjects/untitled1/pic1/20.jpg', 'im1.sift')

im2 = array(Image.open('C:/Users/13799/PycharmProjects/untitled1/pic1/21.jpg'))
sift.process_image('C:/Users/13799/PycharmProjects/untitled1/pic1/21.jpg', 'im2.sift')

l1, d1 = sift.read_features_from_file('im1.sift')
l2, d2 = sift.read_features_from_file('im2.sift')

matches = sift.match_twosided(d1, d2)

ndx = matches.nonzero()[0]
x1 = homography.make_homog(l1[ndx, :2].T)  # 将点集转化为齐次坐标表示
ndx2 = [int(matches[i]) for i in ndx]
x2 = homography.make_homog(l2[ndx2, :2].T)  # 将点集转化为齐次坐标表示

d1n = d1[ndx]
d2n = d2[ndx2]
x1n = x1.copy()
x2n = x2.copy()

figure(figsize=(16, 16))
sift.plot_matches(im1, im2, l1, l2, matches, True)  # 可视化
show()


def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
    """
    使用RANSAC从点对应中稳健估计基本矩阵F.
  （来自http://www.scipy.org/Cookbook/RANSAC的ransac.py）。
    input: x1, x2 (3*n arrays) points in hom. coordinates. """

    from PCV.tools import ransac
    data = np.vstack((x1, x2))
    d = 10  # 20 is the original
    # 计算F并返回inlier索引
    F, ransac_data = ransac.ransac(data.T, model,8, maxiter, match_threshold, d, return_all=True)
    return F, ransac_data['inliers']


# 通过RANSAC找到F.
model = sfm.RansacModel()
F, inliers = F_from_ransac(x1n, x2n, model, maxiter=5000, match_threshold=1e-3)

P1 = array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2 = sfm.compute_P_from_fundamental(F)  # 计算第二个相机矩阵

# print P2
print 'F is'
print F

X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2)

# 绘制X的投影
cam1 = camera.Camera(P1)
cam2 = camera.Camera(P2)
x1p = cam1.project(X)
x2p = cam2.project(X)

figure(figsize=(16, 16))
imj = sift.appendimages(im1, im2)
imj = vstack((imj, imj))

imshow(imj)

cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1p[0])):
    if (0 <= x1p[0][i] < cols1) and (0 <= x2p[0][i] < cols1) and (0 <= x1p[1][i] < rows1) and (0 <= x2p[1][i] < rows1):
        plot([x1p[0][i], x2p[0][i] + cols1], [x1p[1][i], x2p[1][i]], 'c')
axis('off')
show()

d1p = d1n[inliers]
d2p = d2n[inliers]

1、左右拍摄，极点位于图像平面上

7点：

8点经过ransac删除误配后的投影

10点：

两幅图的极点极线：


所求出来的基础矩阵：

2、像平面接近平行，极点位于无穷远

7点：

8点经过ransac特征匹配后的投影：

极点极线：

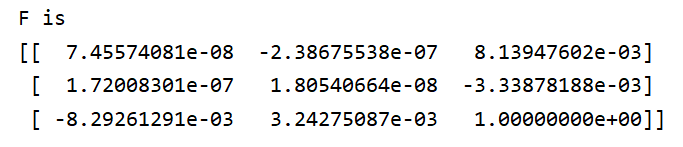
3、图像拍摄位置位于前后

7点：

8点：

10点：

4、结果分析

本次实验先通过sift特征匹配找到匹配点，然后通过ransac匹配去除误匹配，之后再进行基础矩阵求解。通过以上的结果显示，可以发现图像的特征匹配的准确度室外距离相近的图像会高于室外距离不同的图像和室内的图像。在左右拍摄的图片中极点会交于平面中，在平移拍摄的图片中，极点会交于一个极远的位置，在图片中显示不出来。在远近拍摄的图片中，极点会交会于图中的一点。

三、实验中遇到的问题

在选择左右的图片进行匹配时，出现了这个错误，后来发现是图片的问题，拍摄的角度太大，导致最后ransac匹配后不存在匹配点。再重新拍摄了之后就解决了这个问题。