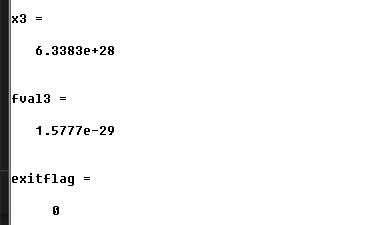Matlab优化算法-非线性规划

非线性规划(NLP)

有约束条件的非线性规划

非线性规划_NLP_1.png

例题1

非线性规划_NLP_2.png

% 非线性规划NLP
%如果目标函数或约束条件中包含非线性函数，就称这种规划问题为非线性规划问题。
%{
[x,fval,exitflag,output,lambda,grad,hessian]= fmincon('fun',x0,A,b,Aeq,beq,VLB,VUB,'nonlcon',options）
其中，大部分参数同线性规划；
    VLB和UVB分别是变量x的下界和上界；
    "fun'为用M文件定义的目标函数F(x)；
“nonlcon'为用M文件定义的非线性向量函数[C(x),Ceq(x)]。
A，b，Aeq，beq定义了线性约束A.x<b，Aeq.x =beq，
如果没有线性约束，则A=[]，b=[]，Aeq =[]，beq =[]；
%}
function func_1 = fun1(x)
    func_1 = x(1)^2+x(2)^2+8;
end

function [C,Ceq] = fun2(x)
    C = -x(1)^2+x(2);   %matlab标准，不等式通通都是小于号 所以取负号
    Ceq = x(1)+x(2)^2-2;
end

x0 = rand(2,1);
VLB = zeros(2,1);
[x,fval,exitflag,output,lambda,grad,hessian]= fmincon('fun1',x0,[],[],[],[],VLB,[],'fun2')
lingo

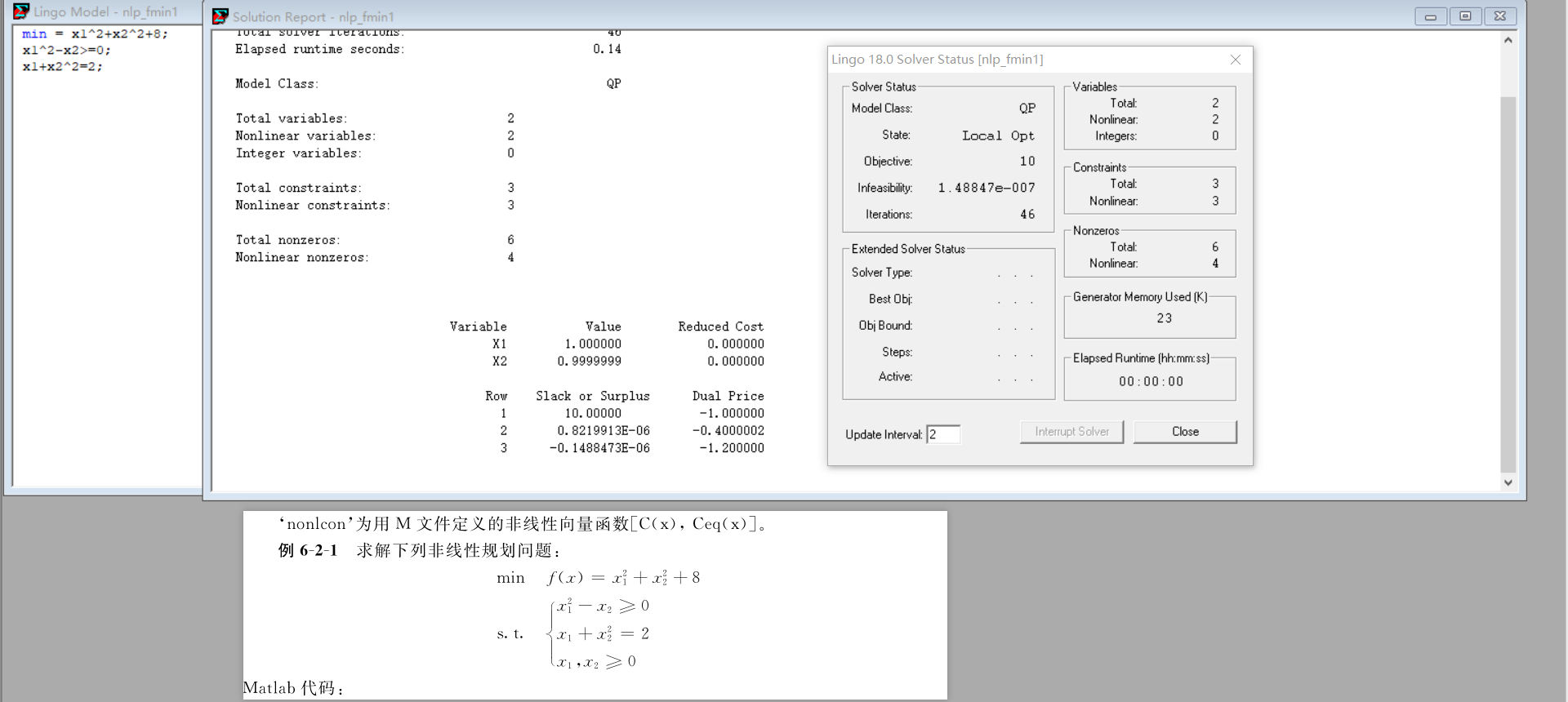
非线性规划_NLP_2 Lingo.png

例题2

非线性规划_NLP_3.png

% 非线性规划NLP
%如果目标函数或约束条件中包含非线性函数，就称这种规划问题为非线性规划问题。
%{
[x,fval,exitflag,output,lambda,grad,hessian]= fmincon('fun',x0,A,b,Aeq,beq,VLB,VUB,'nonlcon',options)
其中，大部分参数同线性规划；
    VLB和UVB分别是变量x的下界和上界；
    "fun'为用M文件定义的目标函数F(x)；
“nonlcon'为用M文件定义的非线性向量函数[C(x),Ceq(x)]。
A，b，Aeq，beq定义了线性约束A.x<b，Aeq.x =beq，
如果没有线性约束，则A=[]，b=[]，Aeq =[]，beq =[]；
%}
%目标函数

function fun_c = fun_c1(x)
    fun_c = x(1)^2+x(2)^2+x(3)^2+8;  %f(x)= x1^2+x2^2+x3^2+8
end

% 非线性函数
function [fun_c,fun_ceq] = fun_c2(x)
    fun_c = [-x(1)^2+x(2)-x(3)^2 , x(1)+x(2)^2+x(3)^2-20]; %大于号转换小于号 写成符号
    %非线性约束条件 函数表达式 不等式矩阵
    fun_ceq = [-x(1)-x(2)^2+2 , x(2)+2*x(3)^2-3];
    %非线性约束条件 函数表达式 等式矩阵
end

x0_1= rand(3,1);
VLB1 = zeros(3,1);
[x,fval]= fmincon('fun_c1',x0_1,[],[],[],[],VLB1,[],'fun_c2')
例题3

非线性规划_NLP_5.png
非线性规划_NLP_6.png
非线性规划_NLP_7.png

二次规划

若某非线性规划的目标函数为自变量x的二次函数，约束条件又全是线性的，则称这种规划为二次规划。

    min 1/2*(x)'H(x)+(f)'x %‘'’ 单引号表示转置符号
    %二次型换实对称矩阵时,需要把矩阵元素扩大2倍
    %eg: f = 2*x1^2-4*x1*x2+4*x2^2-6*x1-3*x2  %只需要看二次型，和交互项
    %实对称矩阵 [2,-2;-2,2] 二次项系数不变化，交互项减半 
    %在调用二次规划函数时,需要把实对称矩阵变成2倍

二次规划1.png
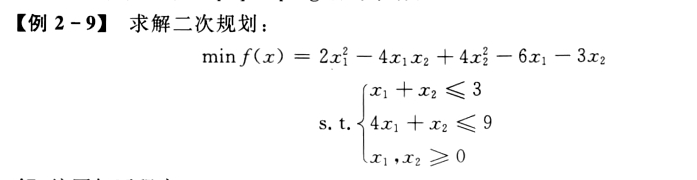
二次规划2.png

%二次规划(线性代数 二次型)(题目见--优化算法-非线性规划.md)
%{
[x,fval,exitflag，output] = quadprog(H,f,A,b,Aeq,beq,LB,UB,x0,options)
\其中，大部分参数同线性规划；
    LB和VB分别是变量x的下界和上界；
    A和b对应不等式约束Ax<b；
    Aeq和beq对应等式约束Ax=b；
    H %实对称矩阵的2倍
    f %一次项系数
    x0为x的初始值；options为控制参数。
%}
%二次型换实对称矩阵

Hx2 = 2*[2,-2;-2,4]; %实对称矩阵
fx2 = [-6,-3];%一次项系数
Ax2 = [1,1;4,1];%不等式约束条件
bx2 = [3;9];%不等式约束条件

[x,fval,exitflag] = quadprog(Hx2,fx2,Ax2,bx2,[],[],zeros(2,1))

无约束条件的非线性规划

  1. fminbnd 查找单变量函数在定区间上的最小值
    fminbnd.png
x = fminbnd(fun,x1,x2) 返回一个值 x，该值是 fun 中描述的标量值函数在区间 x1 < x < x2 中的局部最小值。
  1. fminunc 求无约束多变量函数的最小值
[x,fval,exitflag,output,lambda,grad,hessian]= fmincon('fun',x0,options)
options参数：
        LargeScale，on或off设置大型中型优化算法；
        HessUpdate，设置中型优化算法的搜索方向的算法。
        'bfgs'（默认）为拟牛顿法的BFGS公式；
        'dfp'为拟牛顿法的DFP公式；
        'steepdesc'为最速下降法；
        LineSearchType，设置中型优化算法的步长一维搜索的两种算法。
        'quadcubic'（默认）为混合的二次和三次多项式插值；
        'cubicpoly'为三次多项式插值。
  1. fminsearch 使用无导数法计算无约束的多变量函数的最小值
    fminsearch.png
x = fminsearch(fun,x0) 在点 x0 处开始并尝试求 fun 中描述的函数的局部最小值 x。
%无约束条件的非线性规划(题目见--优化算法-非线性规划.md)
%绘制图像
f3x = linspace(-pi, pi);
y3x = abs(1./(f3x));
plot(f3x, y3x,'ro');
grid on

x3_0 =1;%初值
x3_1 =-3;
x3_2 =1;
[x1,fval1,exitflag] = fminbnd(@fun3, x3_1, x3_2) %在x3_1~x3_2之间的最值
[x2,fval2,exitflag] = fminunc(@fun3, x3_0)
[x3,fval3,exitflag] = fminsearch(@fun3, x3_0)
函数说明

(1)三个函数可能只输出局部最优解。
(2)三个函数均只对变量为实数的问题进行优化。
(3) fminunc函数要求目标函数必须连续。

例题（3种类型函数求解）

fminpro.png
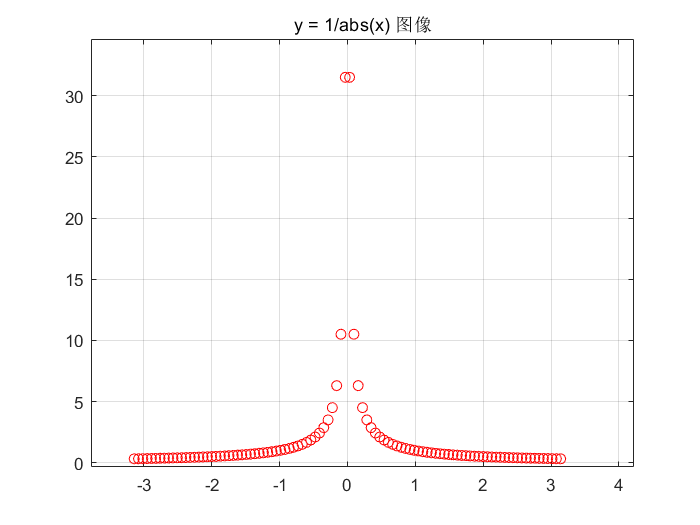
abs.png

%无约束条件的非线性规划(题目见--优化算法-非线性规划.md)
%绘制图像
f3x = linspace(-pi, pi);
y3x = abs(1./(f3x));
plot(f3x, y3x,'ro');
grid on

x3_0 =1;%初值
x3_1 =-3;
x3_2 =1;
[x1,fval1,exitflag] = fminbnd(@fun3, x3_1, x3_2) %在x3_1~x3_2之间的最值
%fminunc函数优化成功，但解是错误的（fminunc的目标函数必须是连续函数，本例目标函数不连续）
[x2,fval2,exitflag] = fminunc(@fun3, x3_0)
%fminsearch函数优化失败，因为该函数只能求解多变量目标函数。
[x3,fval3,exitflag] = fminsearch(@fun3, x3_0)

fminbnd1.png
fminunc.png
fminsearch2.png