【计算机视觉 | 目标检测】术语理解7：二值匹配（Binary Matching），DETR中的Object query的理解，匈牙利算法，DETR中的二分图匹配

文章目录

一、二值匹配（Binary Matching）
二、DETR中的Object query的理解
三、匈牙利算法
四、DETR中的二分图匹配

一、二值匹配（Binary Matching）

当涉及到计算机视觉中的二值匹配（Binary Matching），它是一种用于比较和匹配二值图像的技术。二值图像由黑色和白色像素组成，每个像素只有两种可能的取值。二值匹配的目标是确定两个二值图像之间的相似度或匹配度。

以下是几种常见的二值匹配方法：

汉明距离：通过逐像素比较两个二值图像，计算它们之间的汉明距离。汉明距离是指两个等长字符串之间对应位置不同字符的个数。对于二值图像，可以将每个像素看作一个字符，并计算不同像素的个数。
结构化匹配：将二值图像分割成小的区域或块，并比较它们之间的结构和特征。常见的结构化匹配方法包括形态学操作（如腐蚀、膨胀、开运算、闭运算等）、连通区域分析和轮廓匹配。
特征描述子匹配：通过提取图像中的特征描述子，如局部二进制模式（Local Binary Patterns，LBP）、方向梯度直方图（Histogram of Oriented Gradients，HOG）等，并使用相应的匹配算法进行比较。这些特征描述子能够捕捉图像的局部纹理和形状信息，用于匹配和识别。
模板匹配：将一个小的二值模板图像与待匹配图像进行滑动窗口的方式进行比较。通过计算模板与图像区域之间的相似度来确定匹配位置。常见的模板匹配方法包括平方差匹配、归一化互相关匹配和相位相关匹配。

这些方法的选择取决于具体的应用场景和任务需求。在实际应用中，可能需要根据图像的特征、噪声水平、计算效率等因素进行权衡和选择合适的匹配方法。

二值匹配在计算机视觉中有多种具体的作用和应用。下面列举了其中几个常见的应用场景：

对象识别与分类：二值匹配可以用于对象识别和分类任务。通过比较待识别对象与已知模板或参考对象的二值表示，可以判断它们是否相似或匹配。这在图像检索、目标跟踪、物体识别等任务中都有应用。
特征匹配与配准：在图像配准和特征匹配中，二值匹配常常用于检测两个图像中相同或相似的特征点。通过比较两幅图像的二值表示，可以找到相似的特征区域，并进行配准或匹配。这在图像拼接、摄像头标定、姿态估计等任务中被广泛应用。
目标检测与边界框匹配：在目标检测中，二值匹配可以用于检测和匹配目标物体的边界框。通过比较待检测区域与预定义的二值模板或模式，可以确定是否存在目标物体，并找到其位置和边界框。
形状识别与轮廓匹配：二值匹配在形状识别和轮廓匹配中也发挥着重要作用。通过比较图像的二值轮廓或形状描述子，可以判断两个图像之间的形状相似度，并进行形状识别和匹配。

总的来说，二值匹配在计算机视觉中用于比较和匹配二值图像，以实现对象识别、特征匹配、目标检测、形状识别等多种任务。它提供了一种有效的方式来量化图像之间的相似度，并帮助计算机理解和分析图像内容。

二、DETR中的Object query的理解

在DETR（Detection Transformer）模型中，“Object query” 是指一组特殊的可学习参数，用于在目标检测任务中查询和定位目标物体。它是通过Transformer的自注意力机制（self-attention mechanism）来实现的。

DETR模型的整体结构包括编码器（Encoder）和解码器（Decoder）。编码器将输入图像转换为一系列特征向量，而解码器则使用这些特征向量来生成目标检测的结果。

在解码器中，“Object query” 扮演着关键的角色。它们是一组可学习的向量，每个向量代表一个潜在的目标物体或目标类别。这些向量通常初始化为随机值，然后在训练过程中通过反向传播进行优化。

在解码器的每个解码层，“Object query” 与编码器的特征向量进行自注意力操作，以便将其关联到输入图像中的特定位置和目标物体。这种自注意力机制可以帮助模型学习目标物体在图像中的位置和特征表示。

通过在每个解码层使用多头自注意力机制，DETR模型可以将输入图像的不同区域和目标物体与对应的 “Object query” 进行交互。这样，模型可以同时对整个图像和特定目标物体进行全局和局部的注意力聚焦，从而实现目标的检测和定位。

总的来说，“Object query” 在DETR模型中用于查询和定位目标物体，通过自注意力机制与输入图像的特征进行交互，以实现目标检测任务。它们在解码器的每个解码层起到关键的作用，帮助模型关注特定目标并生成相应的检测结果。

更多理解，详细看我的博客：

https://blog.csdn.net/wzk4869/article/details/129908100

在这里插入图片描述

三、匈牙利算法

匈牙利算法（Hungarian algorithm），也称为Kuhn-Munkres算法，是一种经典的最优匹配算法，用于解决指派问题（Assignment Problem），特别是在二分图中求解最佳的完美匹配（Perfect Matching）问题。

指派问题是在给定的两组元素之间建立最佳的对应关系，其中每个元素必须恰好与另一组中的一个元素匹配。匈牙利算法解决的是一个特殊情况，即每个元素的匹配权重已知，目标是找到一种匹配方式，使得总权重最小。

匈牙利算法的基本思想是通过增广路径（Augmenting Path）的方式逐步构建匹配，直到找到最优解。它的核心步骤如下：

初始化：对于给定的二分图，首先将匹配设置为空，同时为每个顶点和边分配初始标记（通常为0）。
寻找增广路径：通过寻找增广路径的方式来改善当前的匹配。增广路径是指从未匹配顶点出发，依次经过匹配边和非匹配边，最终达到另一个未匹配顶点的路径。
修改标记：根据找到的增广路径，调整顶点和边的标记，以使得已匹配的顶点的标记增加，未匹配的顶点的标记减小。
更新匹配：根据修改后的标记，更新当前的匹配。对于每个未匹配的顶点，如果它有相等的标记，就将它与相等标记的匹配边关联起来，从而形成更大的匹配。
重复步骤2-4：重复执行步骤2-4，直到无法找到增广路径为止，此时得到的匹配即为最优解。

匈牙利算法的时间复杂度为O(n^3)，其中n是顶点的数量。它在解决最优匹配问题上具有较高的效率和准确性，被广泛应用于任务分配、资源分配、航线规划、机器学习中的最大权匹配等领域。

四、DETR中的二分图匹配

整个DETR的正负样本分配的重点就是使用了二分图匹配，来对预测框与gorund truth进行了一个最佳匹配。那么解决这两个集合之间的一个最佳匹配的方式，使得cost代价最少的问题，就被称为二分图匹配问题。

举一个二分图匹配的例子，如何分配一些工人干一些活，从而能让最后的支出最小。因为每个工人有各自的长处与短处，所以他们干不同活所需要的回报不同，那么最后每个工人对应每个任务就形成了一个n工人与n任务的一个nxn矩阵，这个矩阵称为cost matric。最优二分图匹配的意思就是最后能够找到一个唯一解，能够给每个人都能分配其最擅长的一份工作，使得把这三个工作完成最后的价钱最低。匈牙利算法就是解决二分图匹配问题中一个比较有名的算法。

在这里插入图片描述

那么，在目标检测中，这里的工人就可以看成是集合预测出来的预测框。因为这里有100个，所以就是有100个预测框，而这里的不同任务就对应着ground truth（同样设定为100，如果没有100则用∅填充），最后工人的价钱就是每个预测框与每个ground truth的匹配损失（一般是分类损失与回归损失），这里是损失计算为是：

$L_{match}(y_i, \hat{y_{\sigma}(i)}) = -1_{\{c_i \neq \phi\}}\hat{p_{\sigma_i}}(c_i)+1_{\{c_i \neq \phi\}}L_{box}(b_i, \hat{b_{\sigma(i)}})$

把每个pred与ground truth计算器匹配，把cost matric填充完整，cost matric改变成如下所示：

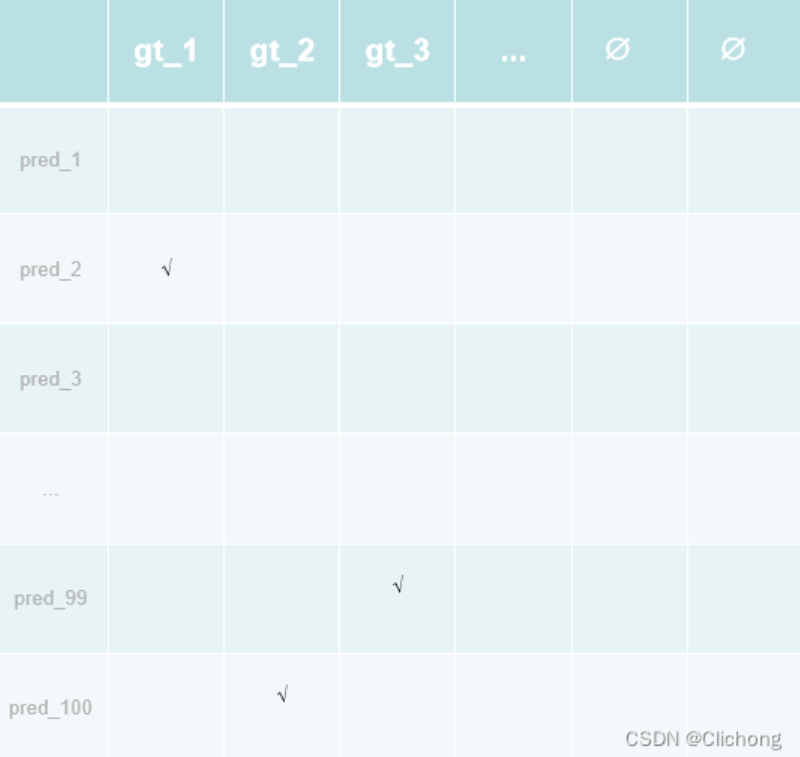
在这里插入图片描述

现在对于这种二分图匹配的问题一般都要成熟的解决方案，比如scipy库中的 linear_sum_assigment 函数。这个函数的输入就是cost matrix，只需要把这个cost matrix传给他，就可以返回每一行（列）应该选择的索引。而且cost matrix也可也是长方形，也不一定是正方形，都是能算出一个最优匹配的。

也就是说，把每个pred与ground truth计算一一匹配的损失，把cost matric填充完整，就可以丢到scipy库中的 linear_sum_assigment 函数中，得到最后的最优解。这里的匹配方式约束更强，一定要得到这个一对一的匹配关系，也就是只有一个框与ground truth的一个框是对应的，这样后面才不需要去做那个后处理nms。

那么一旦知道了这100个框中有哪几个框是跟这个Ground Truth框是对应的，那么接下来就可以算一个真正的目标函数，然后用这个loss去进行梯度传播来更新模型的参数。不够这里是回归损失与分类损失是有改变的，对于分类损失这里去除了log，而对于回归损失是l1 loss与generalized iou loss联合来算bounding box loss。