高级算法设计与分析(四) -- 贪心算法
系列文章目录
目录
前言
tips:这里只是总结,不是教程哈。鉴于本人写字如画符,就不出视频教程了,如实在有需要,请在文章下方留言。当然,文章有任何问题,也请留言,谢谢!
这个系列用另一种形式,把习题放在最下面,看看好用不。
本系列文章最后一文会进行简要全部总结,以及思维导图放在最后一篇文章最下面,请自行获取。
一、贪心算法的基本思想

50,20,0.2,0.1
3*5

二、活动安排问题
1、问题描述
给定一组活动,每个活动都有一个开始时间和结束时间,目标是安排出一个最大数量的相互兼容的活动集合,即这些活动之间不会相互冲突。
2、例子
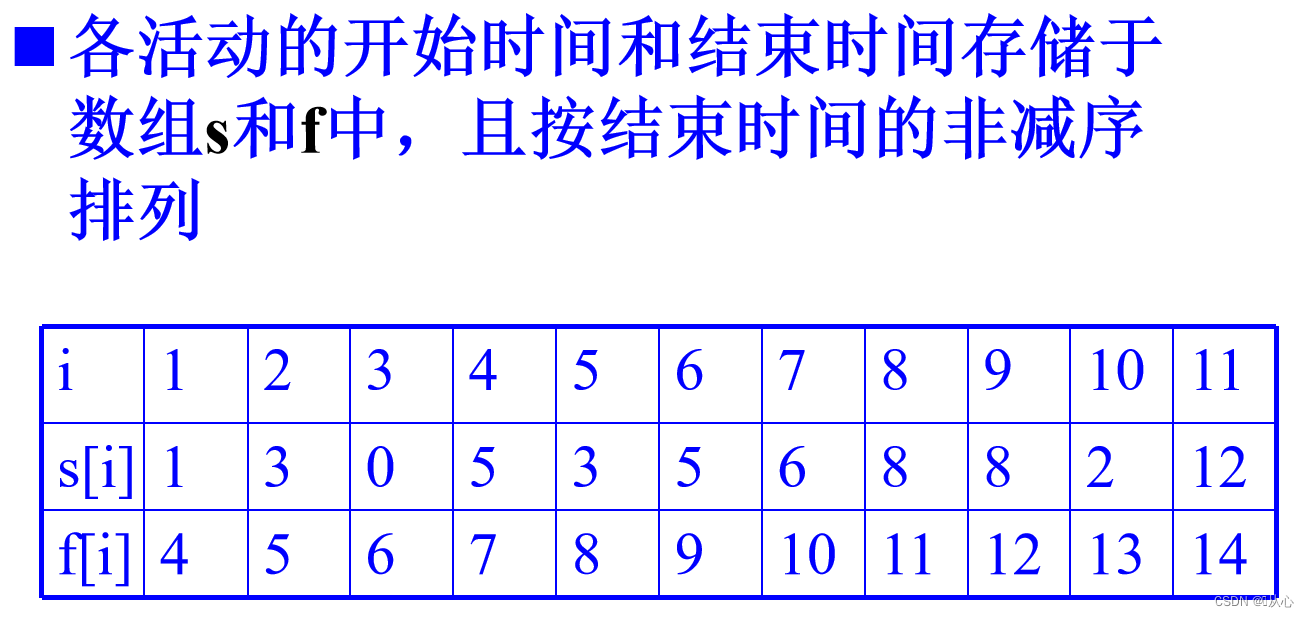
3、步骤:
因为是按照结束时间的非减排序的,选择第一个后(红1),把开始时间在这个活动结束时间之前的都排除(红叉),然后继续选择未排除的结束时间最早的一个(绿2),把开始时间在这个活动结束时间之前的都排除(绿叉),以此类推……
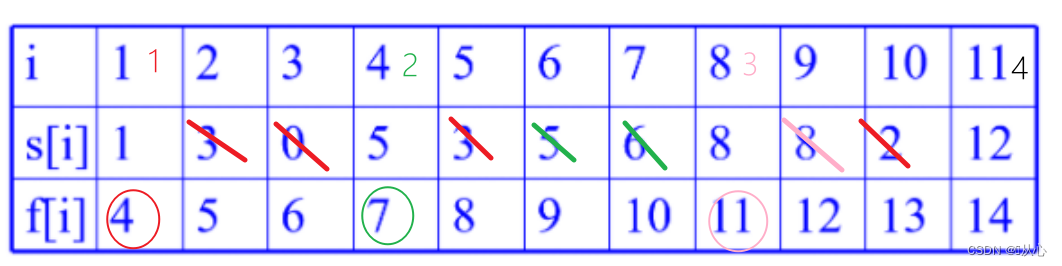
4、算法正确性证明:


另一种表述,看你们能接收那种


三、贪心算法的基本要素
1、贪心选择性质、最优子结构

***自顶向下和自底向上

2、证明方法



4、贪心算法的适用范围

5、背包问题和0-1背包问题


四、哈夫曼编码

复杂度


五、单源最短路径-Dijkstra算法
1、问题描述
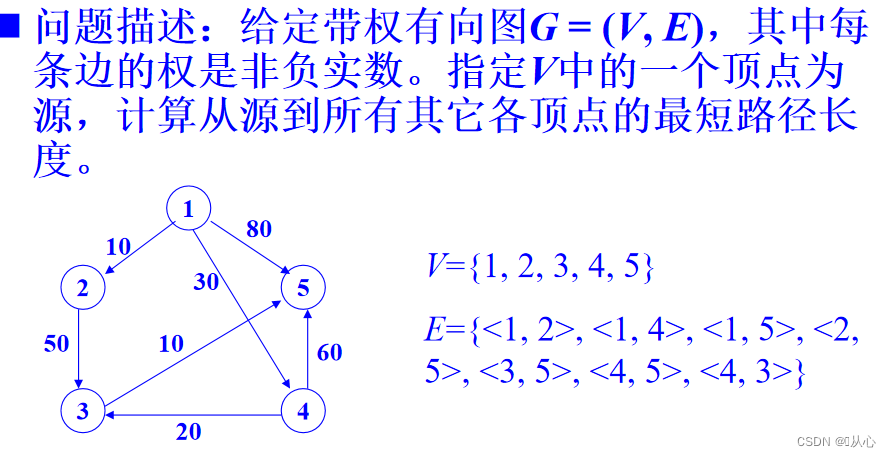

有向图
2、算法的基本思想

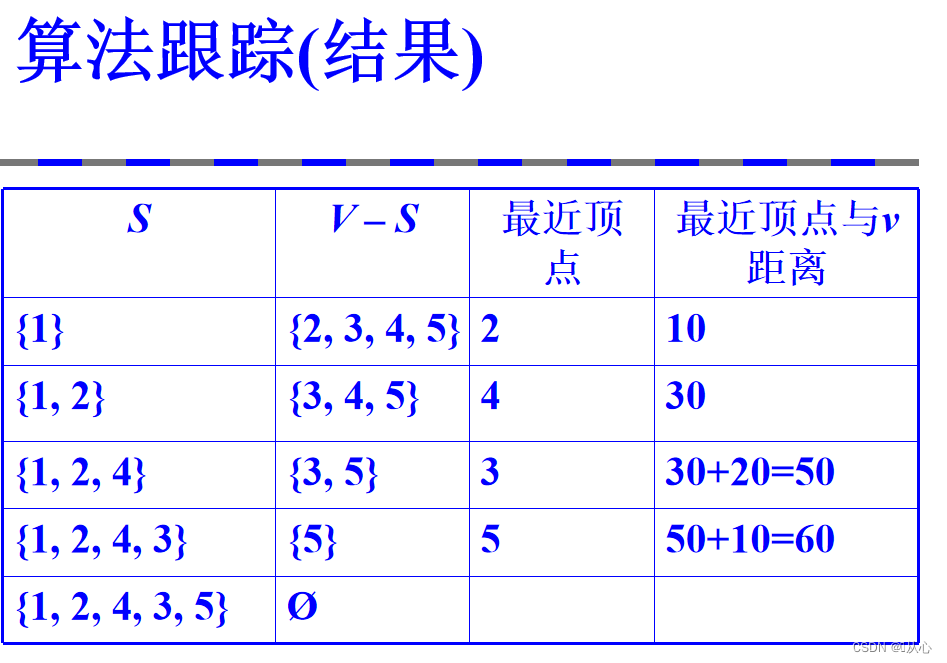
3、将算法用程序描述

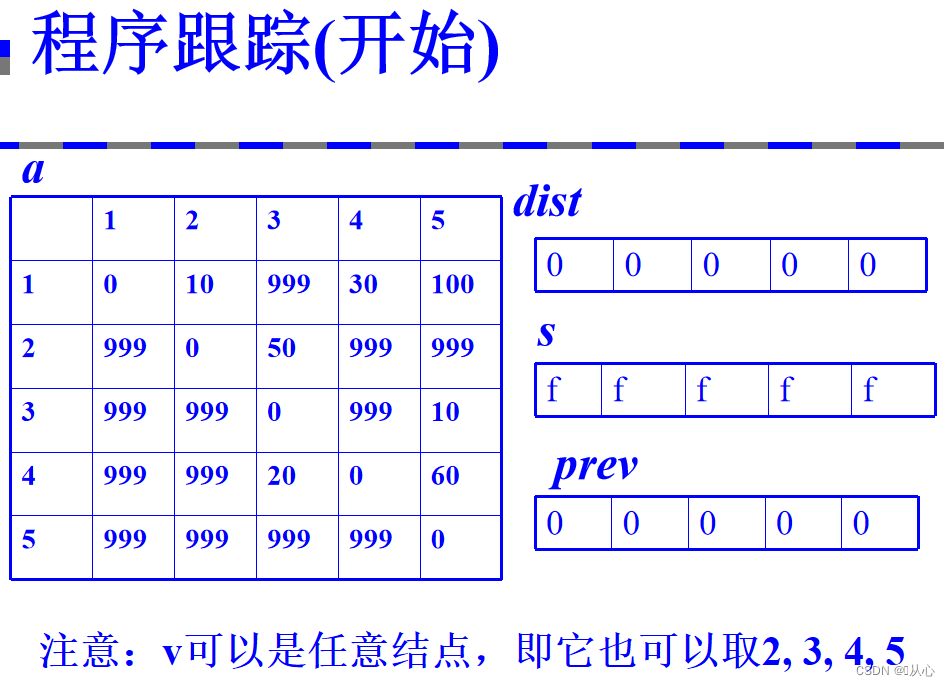
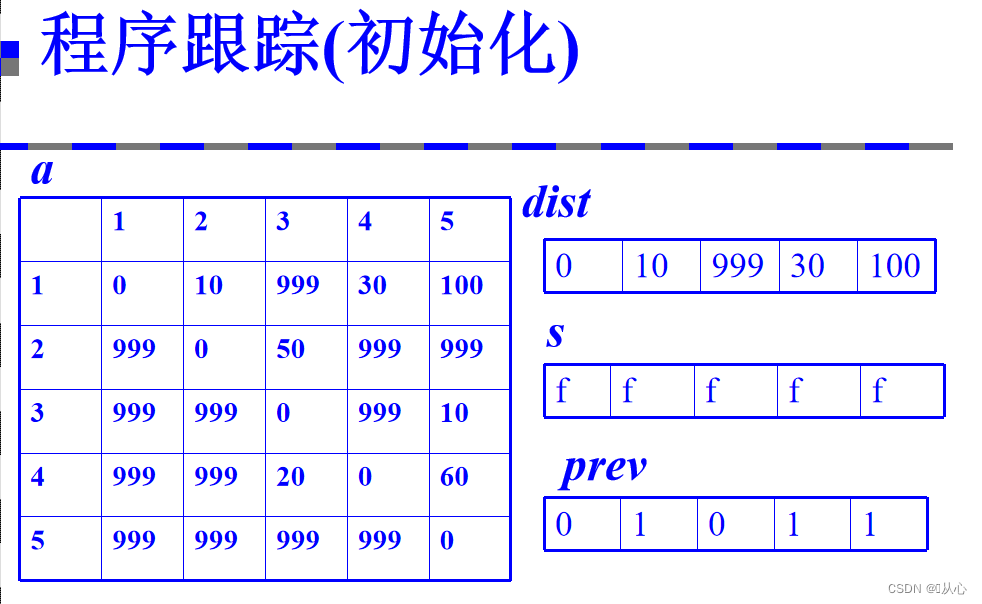
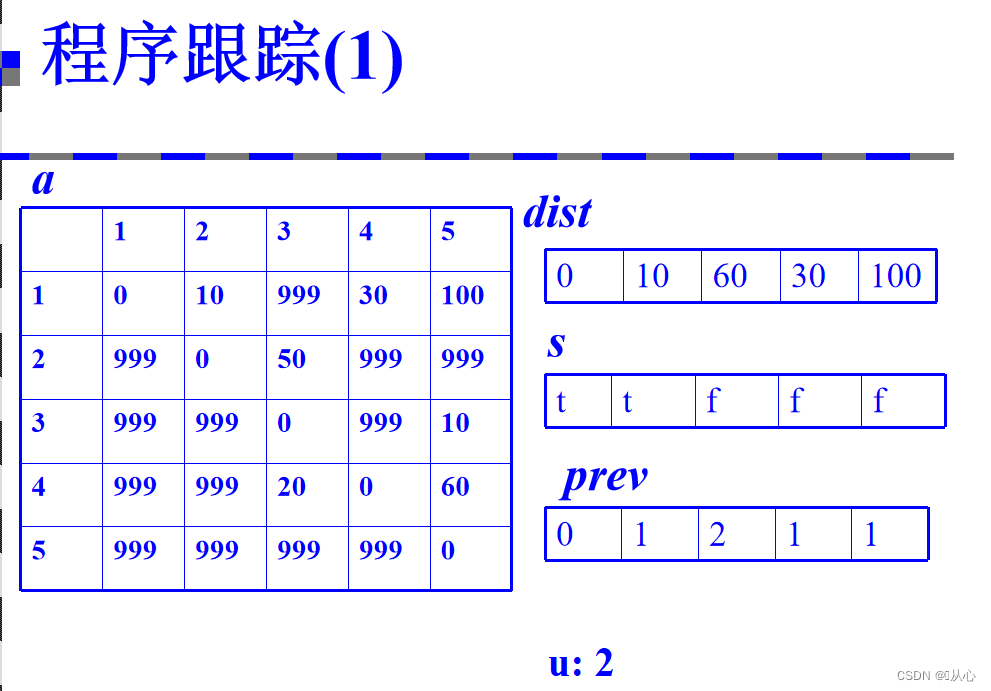
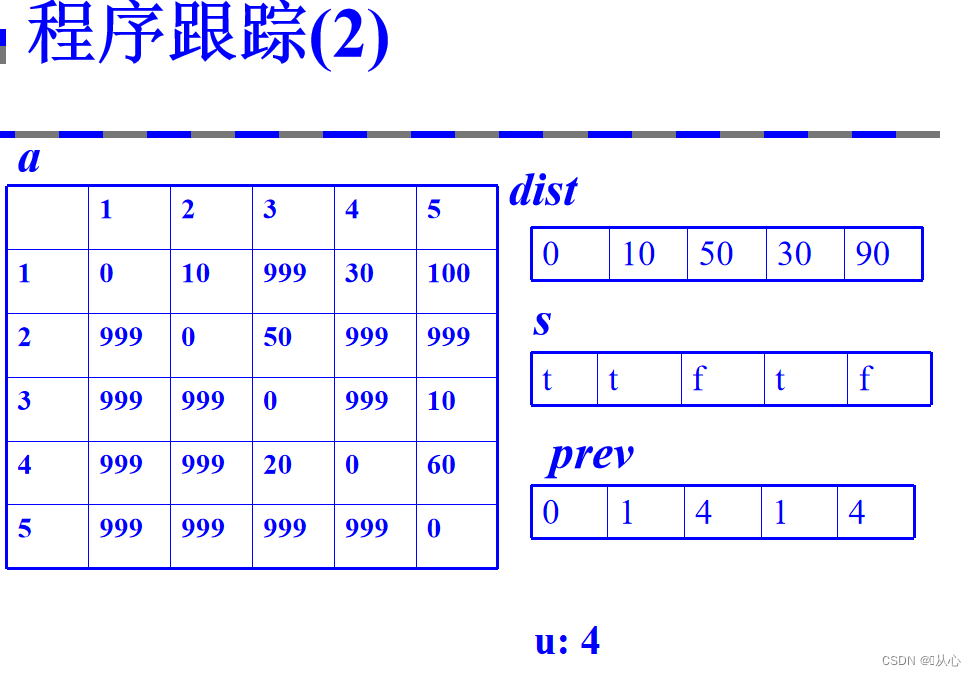
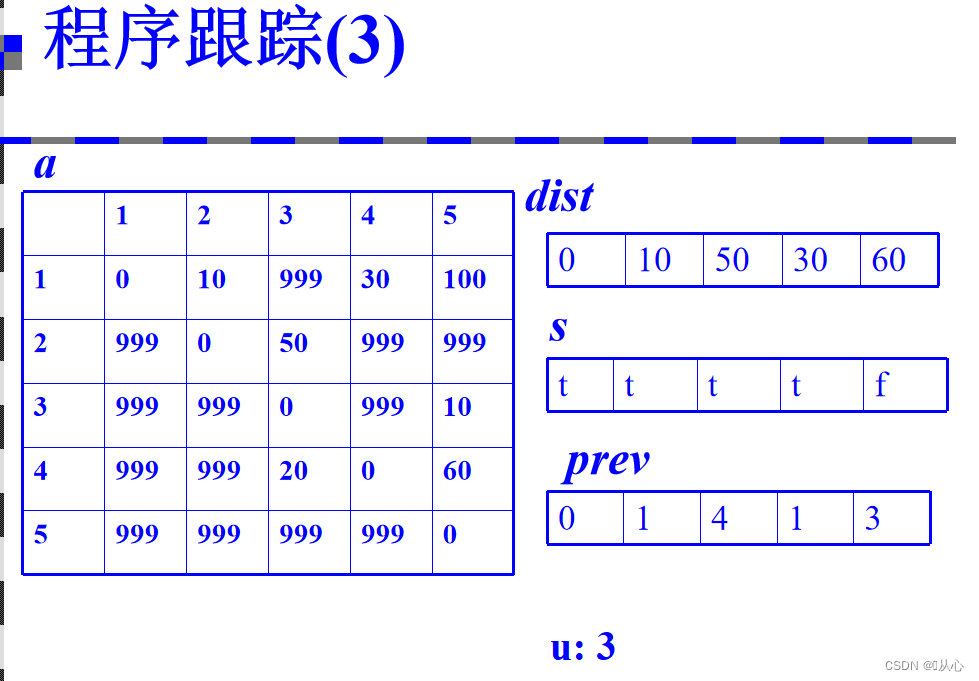
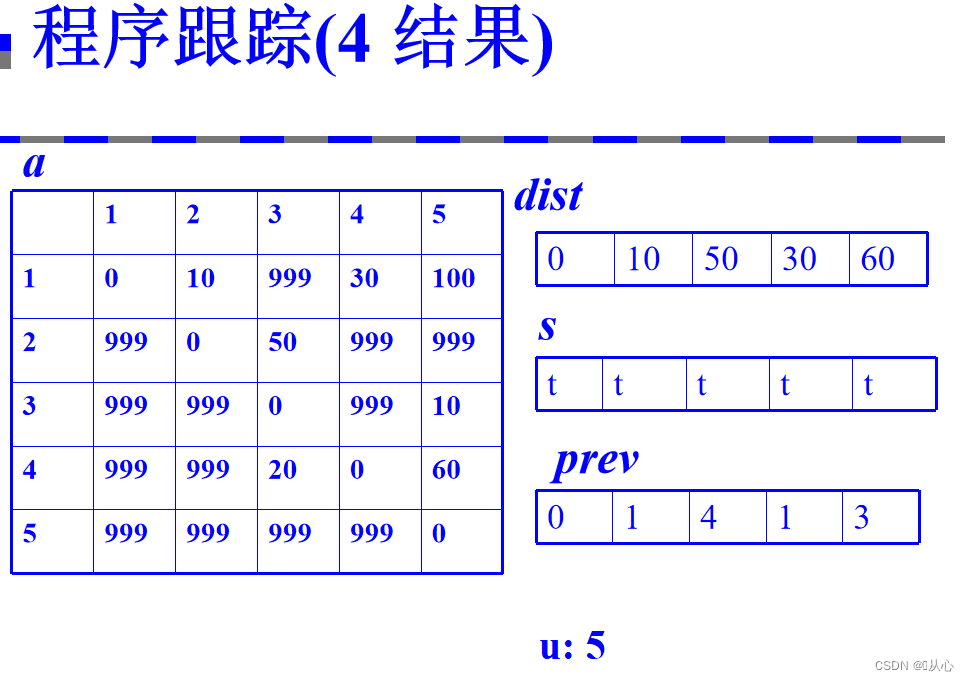
复杂度分析:时间复杂度:o(|V|^2)
4、算法正确性证明


六、最小生成树
1、基础概念与问题


2、prim算法(普里姆算法)

2.1、直接算法实现
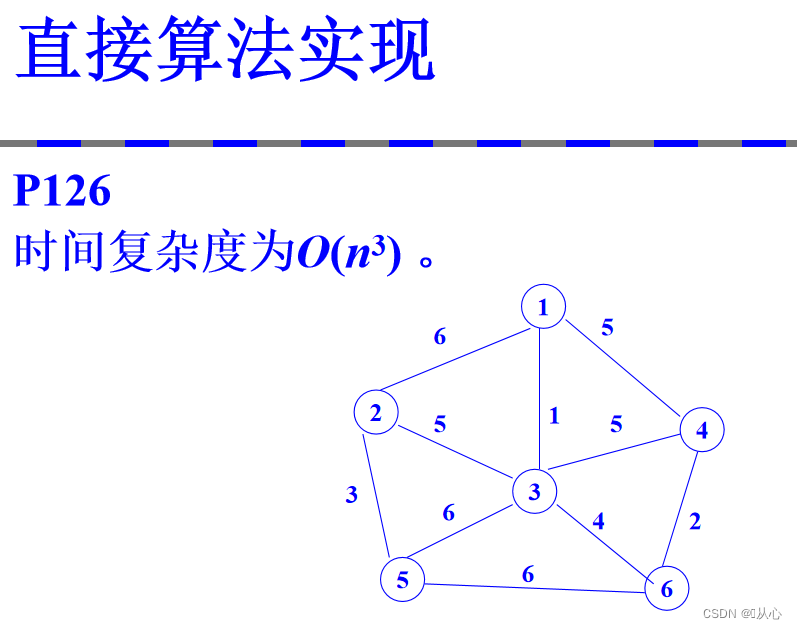
2.2、prim算法实现
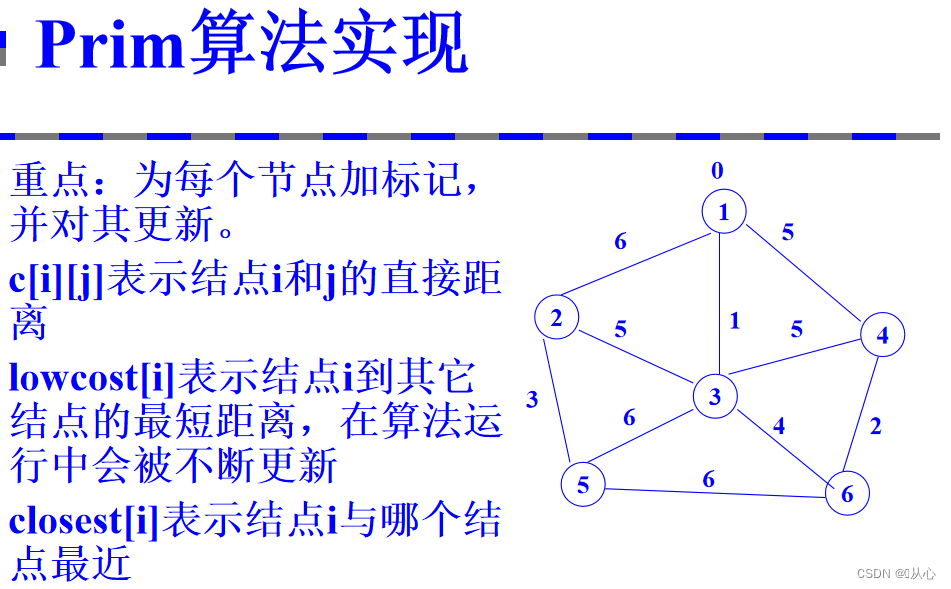
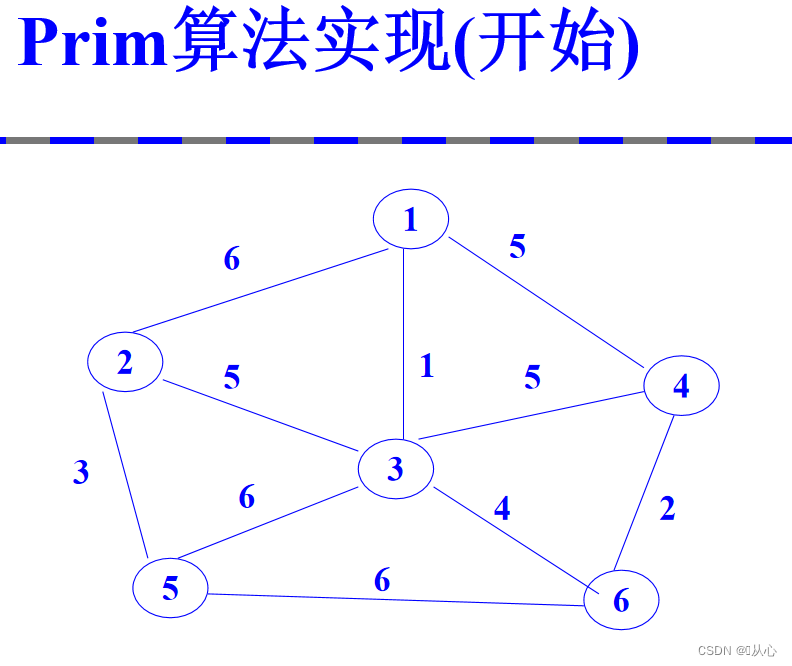
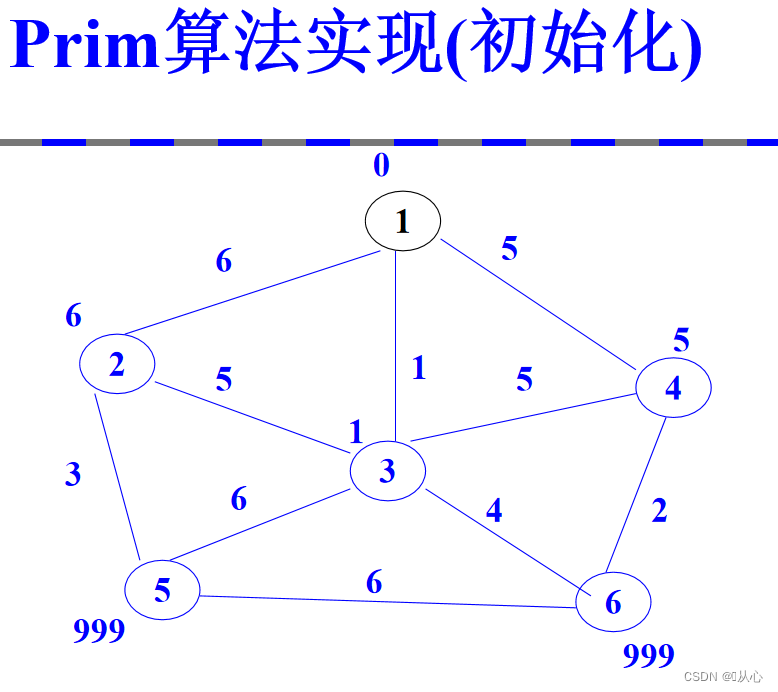
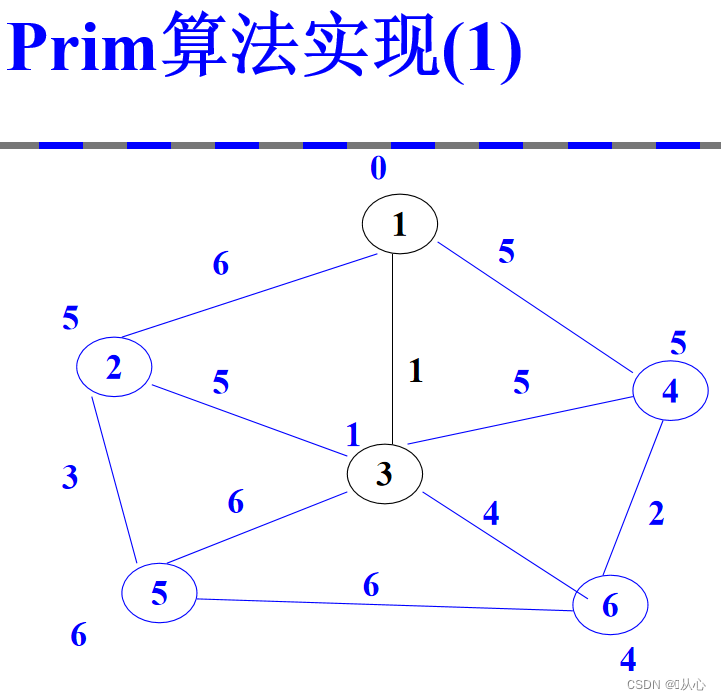
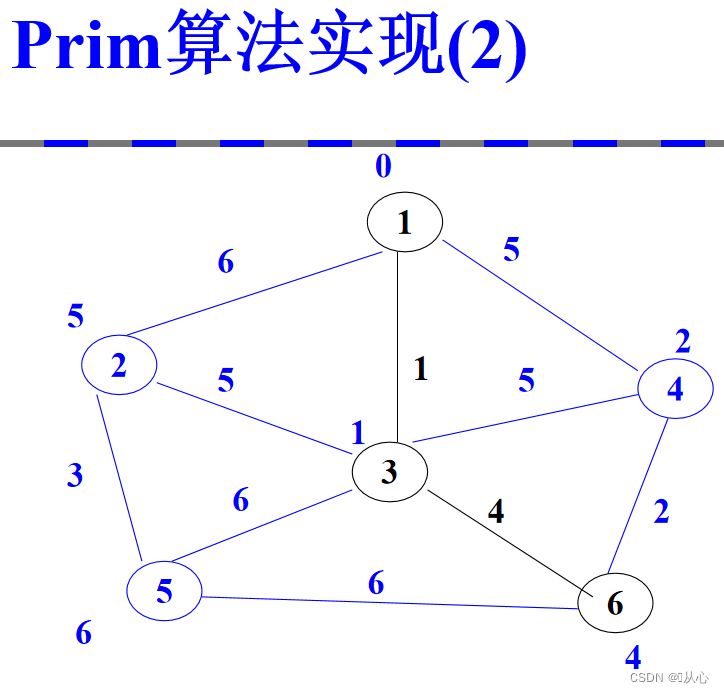
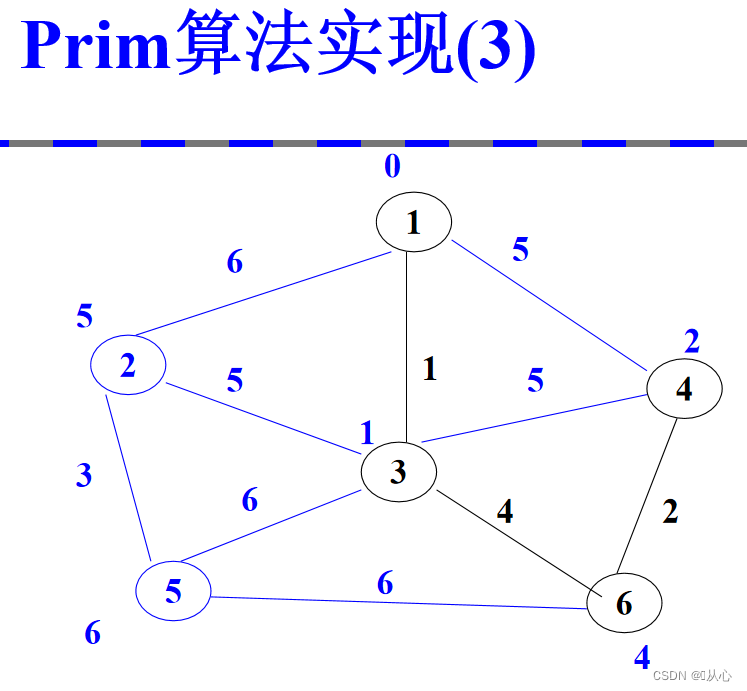
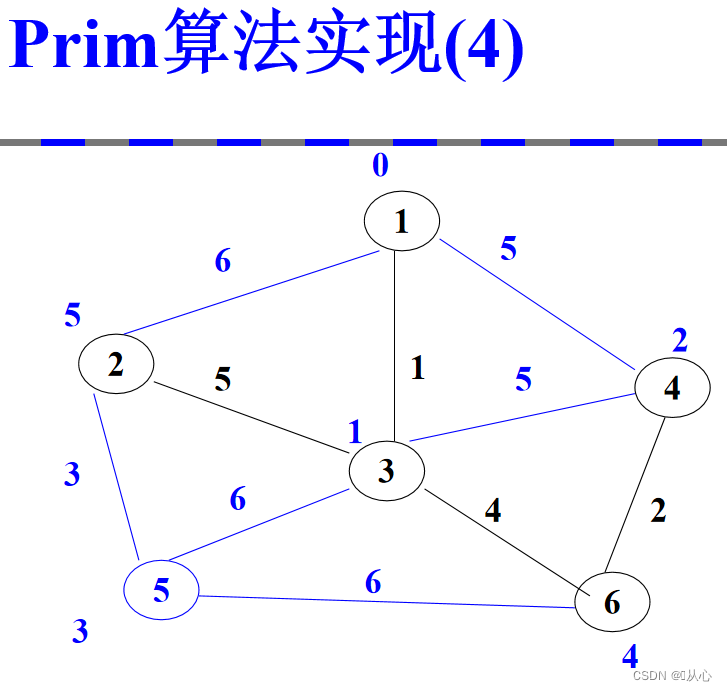
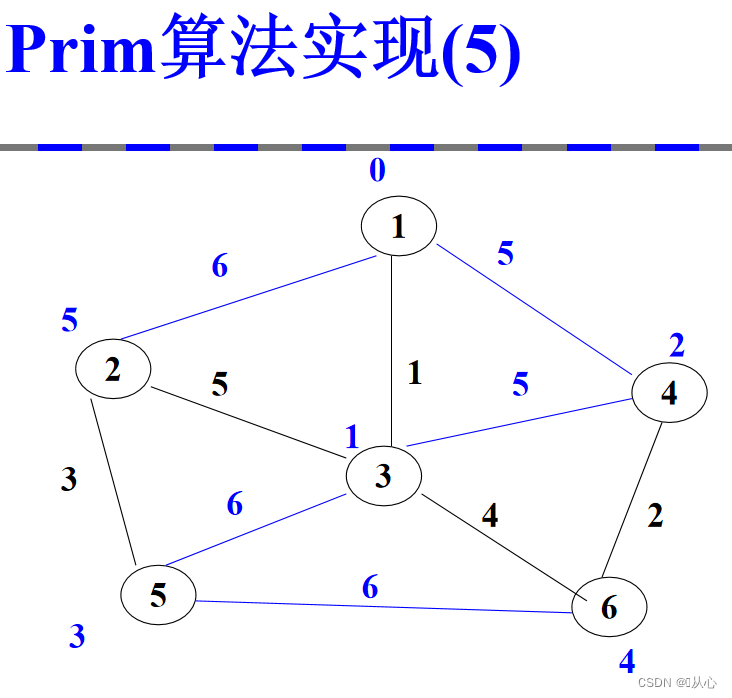
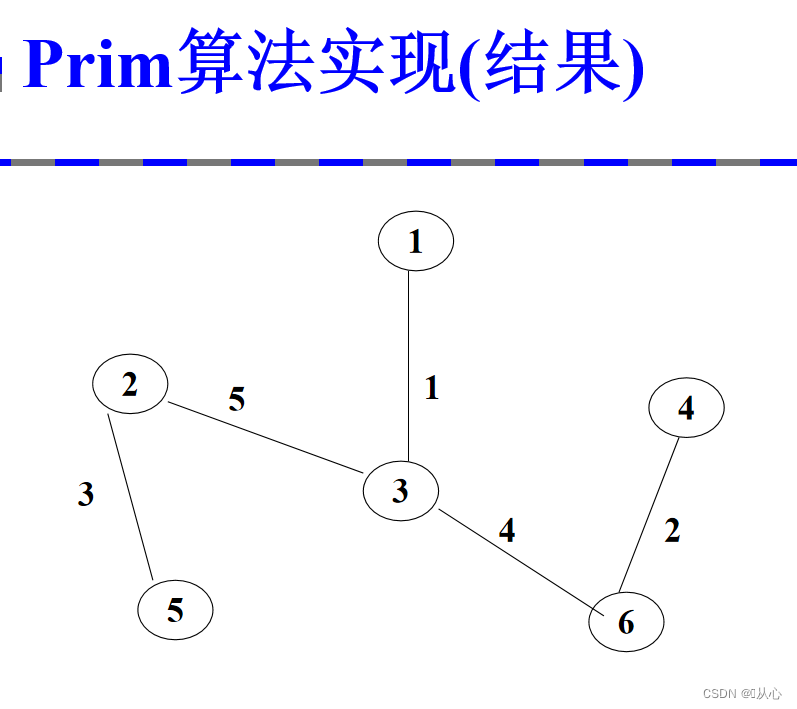
时间复杂度:o(|V|^2)
3、kruskai算法(克鲁斯卡尔算法)

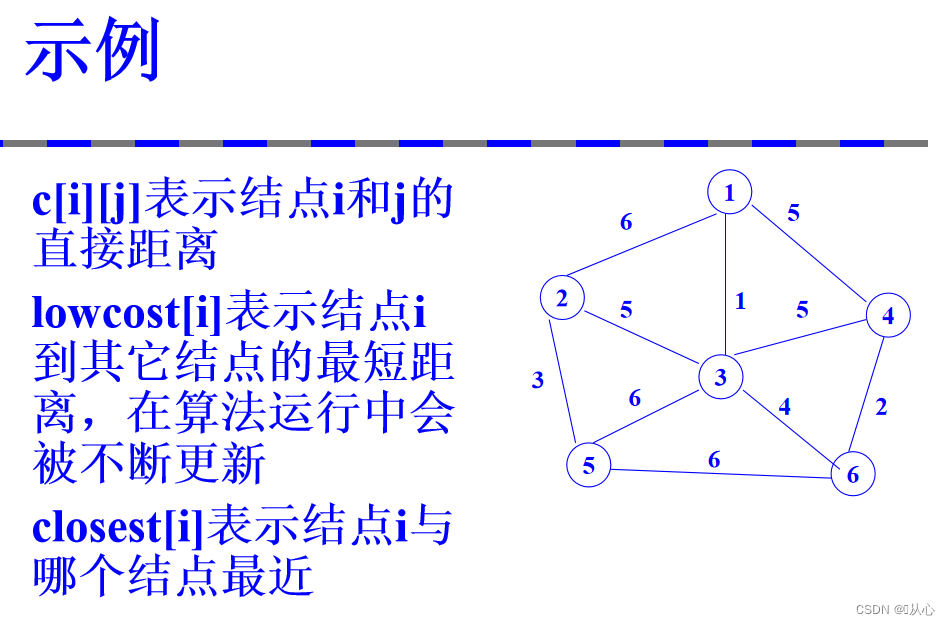

习题
topic1:

topic2:

topic3:

topic4:

topic5:



topic5:
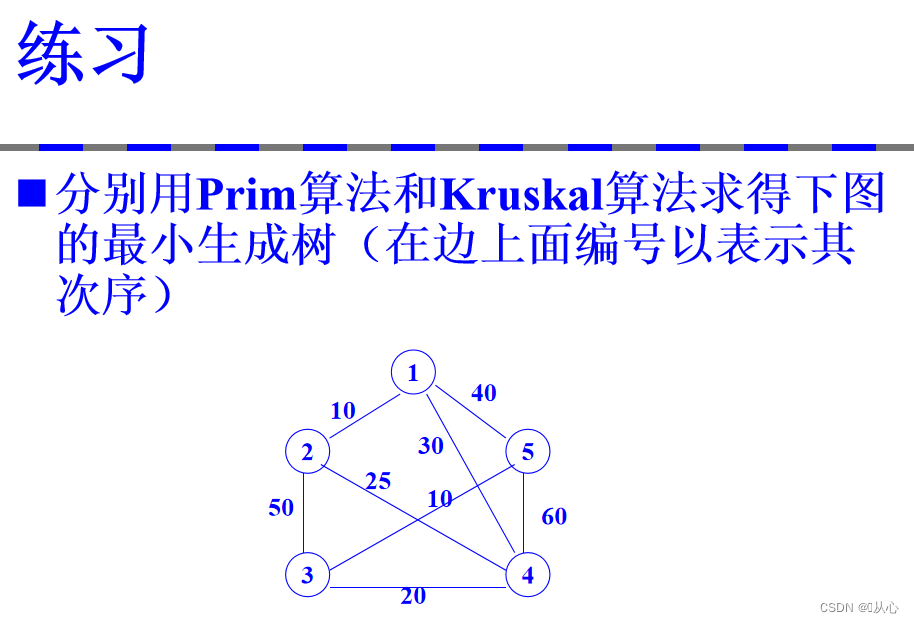
topic6:
