【公式】逻辑回归的损失函数是什么
目录
本文部分图文借鉴自《老饼讲解-机器学习》
一、逻辑回归简介
逻辑回归模型是机器学习中二分类模型中的经典，它的意义在于它能够解决二分类问题，例如判断一个人是否患有某种疾病，或者预测一个事件是否发生等。它是一种广义的线性回归分析模型，推导过程和计算方式类似于回归分析，但实际上主要是用来解决二分类问题。此外，逻辑回归模型还可以处理多分类问题，例如根据多个特征预测一个人所属于的类别等。
逻辑回归模型最终输出属于类别1的概率，它的模型表达式如下：
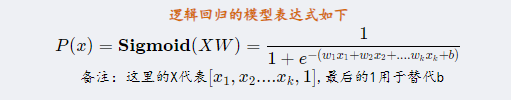
二、逻辑回归模型的损失函数
2.1 损失函数与其意义
在机器学习和优化问题中，损失函数（或目标函数）具有重要的意义。它用于衡量模型预测结果与实际结果之间的差异，从而反映模型的性能和准确度。
损失函数的目标是最小化预测结果与实际标签之间的差异。具体来说，它通过对模型的参数进行优化，使得模型的预测结果更接近于实际的观测结果。如果模型的预测结果与实际观测结果相差较大，那么损失函数的值就会较大；反之，如果预测结果与实际观测结果相差较小，那么损失函数的值就会较小。
通过最小化损失函数，我们可以找到一组最优的模型参数，使得模型能够更好地拟合训练数据，提高模型的准确度和泛化能力。因此，损失函数在逻辑回归模型中具有重要的意义，它是评估模型性能和指导模型优化的关键指标。
2.2 逻辑回归的损失函数
对于逻辑回归模型，损失函数是用来衡量模型预测概率与实际标签之间的差距的。在二分类问题中，逻辑回归模型的预测结果通常被解释为概率值，表示样本属于正类的概率。当这个概率值越接近于1时，表示模型预测样本为正类的可能性越大；反之，当概率值越接近于0时，表示模型预测样本为负类的可能性越大。
在逻辑回归中，常用的损失函数是对数似然损失（Log-Likelihood Loss），也称为交叉熵损失（Cross-Entropy Loss）。逻辑回归的损失函数如下：
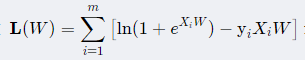
2.3 从交叉熵角度理解逻辑回归的损失函数
交叉熵损失函数的计算基于概率分布之间的差异。在分类问题中，模型的预测结果通常是一个概率分布，表示每个类别上的预测概率。交叉熵损失函数通过比较模型预测的概率分布与实际的标签分布之间的差异来计算损失值。
从交叉熵角度理解逻辑回归的损失函数几乎不需要推导过程，但需要对熵及交叉熵的意义较为熟悉，可以参考文章《老饼讲解|【逻辑回归】逻辑回归损失函数交叉熵形式的理解》
2.4 从对数似然角度推导逻辑回归的损失函数
对数似然损失函数是一种损失函数，主要用于评估分类器的概率输出。它是在概率估计上定义的，通过惩罚错误的分类来实现对分类器准确度的量化。最小化对数似然损失基本等价于最大化分类器的准确度。对数似然损失函数在机器学习和深度学习中广泛应用，特别是在分类问题中，可以有效地衡量模型预测结果的准确性。
从对数似然角度推导逻辑回归的损失函数时，推导思路流程如下：
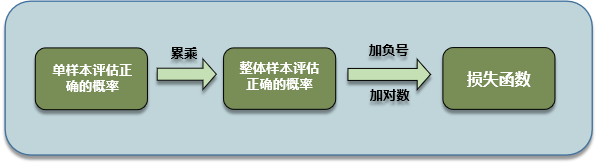
模型对单个样本评估正确的概率为：
上式等价于：
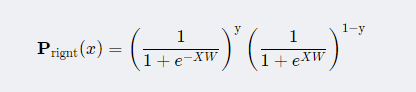
从而整体样本评估正角的概率为：
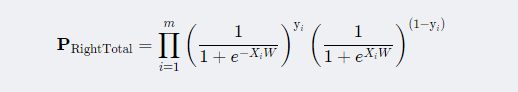
最大化总概率(上式)，即最小化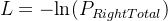
,对其进行化简后就可以得到逻辑回归的操作函数，如下
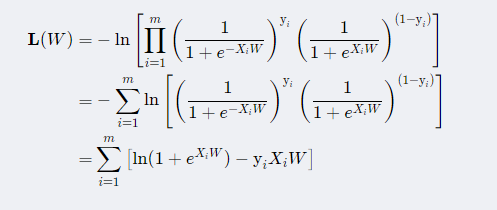
相关细节过程可参考《老饼讲解|【推导】逻辑回归损失函数推导过程》
三、逻辑回归损失函数的梯度
3.1 逻辑回归损失函数的梯度公式
逻辑回归损失函数的意义主要用于求解逻辑回归模型中的参数，通常使用梯度下降等相关算法来进行求解，因此需要算出逻辑回归损失函数的梯度。
逻辑回归损失函数的梯度公式如下：
3.2 用梯度下降法实现逻辑回归的求解
根据以上公式，就可以使用梯度下降算法来求解逻辑回归模型中的参数。
逻辑回归的梯度下降求解方法可以分为以下几个步骤：
1.初始化参数：选择一个初始的参数向量，例如随机初始化。
2.计算损失：根据当前参数计算逻辑回归的损失函数值。
3.计算梯度：根据损失函数计算每个参数对应的梯度。
4.更新参数：根据梯度的大小，更新每个参数的值。
重复步骤2-4直到收敛或达到预设的最大迭代次数。
在具体实现中，逻辑回归的损失函数通常是对数似然损失函数，而梯度下降算法则是通过迭代更新参数来最小化损失函数。每次迭代中，根据当前的参数计算每个样本的预测概率和实际标签的对数似然损失，然后对损失函数求梯度并更新参数。这个过程一直重复，直到损失函数的值收敛或达到预设的最大迭代次数。
下面是python的实现代码示例：
# -*- coding: utf-8 -*-
"""
梯度下降求解逻辑回归
"""
from sklearn.datasets import load_breast_cancer
import numpy as np
#----数据加载------
data = load_breast_cancer()
X = data.data[:,4:8]
y = data.target
#-----给x增加一列1---------
xt = np.insert(X, X.shape[1], 1, axis=1)
#-----梯度下降求解w---------------
np.random.seed(888) # 设定随机种子，以确保每次程序结果一次
w = np.random.rand(xt.shape[1]) # 初始化
for i in range(10000):
p = 1/(1+np.exp(-xt@w)) #计算p
w = w - 0.01*(xt.T@(p-y)) # 往负梯度方向更新w
p = 1/(1+np.exp(-xt@w)) # 最终的预测结果
print("参数w："+str(w))运行后输出结果如下：
参数w：[ 7.16215375 14.98708501 -16.84689114 -73.92486786 3.38331608]
如果觉得本文有帮助，点个赞吧！