NumPy教程（二）—— 数据存储及各种常用方法

1.文件输入和输出

1.1 CSV文件的存取

csv文件的读取（读）

语法：np.loadtxt（frame，dtype=np.float，delimiter=None，unpack=False）

参数： frame：文件、字符串或产生器的名字，可以是.gz或.bz2的压缩文件

dtype：导入时需要将csv文件中的元素由字符串指定为一个固定格式

delimiter：分割字符串，默认是空格（存储CSV文件，要改为逗号）

unpack：读入的属性是否写入不同变量（默认False，写入同一个变量）

将数据写入文件（存）

语法：np.savetxt（frame，array，fmt = ‘%.18e’，delimiter = None）

参数： array：要存入文件的数组

fmt：写入文件时每个元素使用的格式（默认科学计数法保留18位小数） %d：整数

import numpy as np
a = np.arange(100).reshape(5,20)
np.savetxt('a.csv', a, fmt="%d", delimiter=",")  #存储

b = np.loadtxt('a.csv',delimiter=",")  #读取
print(b)

1.2 numpy的便捷文件存取

numpy可以在硬盘中将数据以文本或二进制的形式进行存入硬盘或由硬盘载入

下述函数是numpy高效存取硬盘数据的工具函数

函数	描述
np.save（frame，array）	将数组存储到文件中但必须以.npy为文件名
np.savez（frame，a=arr1, b=arr2）	将多个数组保存到一个文件中必须以.npz为文件名数组以类似键值对形式传入导入时，会得到一个类似字典的对象
np.savez_compressed （frame，a=arr1, b=arr2）	将多个对象存入压缩文件中
np.load（frame）	读取 .npy 或 .npz 格式的数据

import numpy as np
a = np.random.randn(5,5)
b = np.random.randn(3,3)

np.save("a.npy",a)
np.savez("ab.npz",a=a,b=b)

load = np.load("ab.npz")
print(load["a"]) #文件的读取 类似字典

2.利用数组做数据处理的各种方法

2.1 数组代替循环

Numpy数组可以用数组表达式去代替循环，这种方法称作矢量化。它可以大大提升循环速度

案例一：计算 sqrt(x^2+y^2)

np.meshgrid函数：接收两个一维数组，分别复制成两个二维数组

import numpy as np
data1 = np.arange(-5,5,0.1)
data2 = np.arange(-10,0,0.1) #生成两个一维数组
x,y = np.meshgrid(data1,data2) #复制成二维数组
print(x)
z = np.sqrt(x**2 + y**2)
z = np.rint(z) #取整
print(z)

案例二：将条件逻辑表述为数组

np.where（condition，xarr，yarr）：等价于列表推导式 x if condition else y

当condition（布尔类型）的值为Ture时，选取xarr的值，反之选取yarr的值

# 案例：将arr中所有小于0的数替换为0
import numpy as np
arr = np.random.randn(4,4)
arrxin = np.where(arr<0,0,arr)
print(arrxin)

案例三：通过广播将一维数组设置到高维数组的列中

np.newaxis：插入新维度，将一维数组变成二维数组，二维变成三维

# np.newaxis的用法
import numpy as np
x = np.arange(4) # [0 1 2 3]

print(x[np.newaxis,:]) # 插入行 [[0 1 2 3]]
print(x[:,np.newaxis]) # 插入列 [[0]
                       #        [1]
                       #        [2]
                       #        [3]]

# 案例
import numpy as np
old = np.array([1,2,3,4],dtype=int)
new = np.zeros((4,3),dtype=int)

new[:] = old[:,np.newaxis] # 插入列，再利用广播原则
print(new)

2.2 数学和统计方法

下述函数的调用方式全部为 np.函数名（arr）或者 arr.函数名（）

函数	说明	备注
sum、mean、 median	沿轴向计算累计和、均值、中位数	可以接受一个可选参数axis 例如 arr.mean（axis = 1）用于计算给定轴向上的统计值形成一个下降一维度的数组
std、var	标准差和方差
min、max	最小值和最大值
argmin、argmax	最小值和最大值的位置
cumsum	从位置0开始写元素累计和	不返回值，而是返回一个相同长度的数组，写出累计求和/积的中间结果例如：[ 1,2,3 ] 一> 累计和 [ 1,3,6 ] 多维则可指定axis，在轴向上分别计算
cumprod	从位置1开始写元素累计积

2.3 用于排序以及布尔数组的方法

函数	说明	备注
arr.sort（axis=）	按值的大小排序（升序）	多维可指定axis，在轴向上分别排序
sum	在2.2的方法中，布尔值会被转化为1和0；因此我们可以用sum对布尔型数组中的True值计数
arr.any（）	测试数组中是否存在一个或多个True	返回布尔类型值
arr.all（）	测试数组中是否所有值都是True	返回布尔类型值

2.4 集合运算方法

函数	说明
unique（x）	计算x的唯一值，并返回已排序的结果相当于重复的值只保留一个
intersect1d（x，y）	计算交集，并排序
union1d（x，y）	计算并集，并排序
in1d（x，y）	计算x中的元素是否包含在y中，返回一个bool值数组
setdiff1d（x，y）	差集，在x中，但不在y中的 x的元素
setxor1d（x，y）	异或集，在x或y中，但不属于二者交集的元素

3.线性代数函数

为了应对矩阵运算，numpy.linalg提供了一些用于矩阵分解、求逆...之类的函数

使用之前应先导入相应函数：from numpy.linalg import 函数名

函数	说明	备注
diag（x）	将方阵的对角线元素以一维数组形式返回；或将一维数组转化为方阵
x.dot（y）	矩阵乘法	@也可用作矩阵乘法运算符如：X@Y
trace（x）	求迹：对角线元素之和
det（x）	计算矩阵对应的行列式
eig（x）	计算方阵特征值和特征向量返回一个一维数组和一个多维数组
inv（x）	计算方阵的逆	也可直接写 X.T
pinv（x）	计算矩阵的Moore-Penrose伪逆
qr（x）	计算QR分解，返回俩个数组
svd（x）	计算奇异值分解（SVD）
solve（A，b）	求解线性方程组 Ax=b ，其中A为一个方阵
lstsq（A，b）	计算 Ax=b 的最小二乘解

4.伪随机数生成

伪随机数是指由计算机算法生成的随机数，之所以称做伪随机是因为计算机中的随机函数是按照一定算法模拟产生的，其结果是确定的，是可见的。

而真随机是真正随机的数，如人群身高、重复抛硬币等

4.1 seed设置随机数种子

我们可以通过 np.random.seed（任意数字）来设置一个随机数种子，这样可以保证我们每次调用这个文件，里面的随机数输出都是一样的

如果什么都不输入，则默认为系统时间

注意事项

1）设置种子后，是每次运行.py文件的输出结果都一样，而不是每次随机函数生成的结果一样，如下，我们可见a b两次调用random结果不同，但如果再次运行这个文件，结果还是这两个数

import numpy as np
np.random.seed(123)
a = np.random.random()
b = np.random.random()
print(a,b)  # 输出结果为：0.6964691855978616
            #           0.28613933495037946

2）如果想a b两次调用结果都相同，需要在b之前再次设置相同的随机数种子，这是因为种子只会跟第一个碰到的生成器绑定

import numpy as np
np.random.seed(123)
a = np.random.random()
np.random.seed(123)
b = np.random.random()
print(a,b)  # 输出结果为：0.6964691855978616
            #           0.6964691855978616

3）如果设置了随机种子，那么它的作用域将是全局，也就是之后的每一次random都会受他影响，输出一样的数据，如果想取消他的全局影响在后面的生成器采用随机输出，有两种方案

方案一：直接在后续的生成器之前都加上 np.random.seed（）

原理是默认填入系统时间，这样每次操作种子数就都不同，就会重新随机

import numpy as np
np.random.seed(123)
a = np.random.random()
np.random.seed()
b = np.random.random()
print(a,b)  # 输出结果为：0.6964691855978616
            #           不固定

方案二：使用 numpy.random.RandomState生成一个随机数生成器，使其独立于其他随机数

import numpy as np
rng = np.random.RandomState(123)
a = rng.random() #若后续仍要调用，必须使用rng这个前缀

b = np.random.random() #其他的随机数

c =rng.random()  #再次调用这个随机数生成器

rng = np.random.RandomState(123) #再次调用这个随机数生成器种子
d = rng.random()

print(a,b,c,d)  # 输出结果为：0.6964691855978616
              #            不固定
              #            0.28613933495037946
              #            0.6964691855978616

4.2 随机数函数

下述函数的调用方式全部为 np.random.函数名（）

某些函数使用前需要先导入： from random import 函数名

函数	说明

rand（size）	根据size生成 [ 0,1 ] 均匀分布随机数数组
randn（size）	根据size生成标准正态分布随机数数组
randint（low，high，shape）	根据 shape生成 [ low , high ) 之间的随机整数数组如果不输入shape，则生成一个随机整数如果不输入high，则生成 [ 0 , low ) 之间的一个随机整数
shuffle（arr）	根据arr的零轴进行随机排序，且原数组发生改变
permutation（arr）	同上，但创建一个新的数组，原数组不变
chioce（arr，[size,replace,p]）	从一维数组arr中以概率p抽取元素，形成size形状的新数组 replace：是否可以重用元素，默认False；默认等概率
uniform（low，high，size）	根据size生成 [low，high ] 均匀分布随机数数组
normal（loc，scale，size）	根据size生成均值loc，标准差scale 正态分布随机数数组
poission（lam，size）	根据size生成随机事件发生率为lam 的泊松分布随机数数组

4.3 案例

要求：实现1000次的随机漫步

import numpy as np
steps = 1000
draws = np.random.randint(0,2,size=steps)
move = np.where(draws==0,-1,draws)
walk = np.cumsum(move)
print(walk)

# 在数组运算下，我们可以轻易实现很多内容
# 例如：最远距离
print(np.abs(walk).max())
# 第一次到达10或-10时 的位置
print((np.abs(walk) >= 10).argmax())

5.通用函数（了解）

5.1 一元通用函数

下述函数的调用方式全部为 np.函数名（arr）

一元函数	描述
abs fbs	计算各个元素的绝对值，对于非复数，可以使用fbs函数
sqrt	计算各个元素平方根（要求非负）
square	计算各个元素的平方
exp	计算各个元素的自然指数值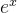 $e^{x}$
log、log10 log2、log1p	分别对应：自然对数（e为底）、10为底、2为底、log（1+x）（要求正数）
sign	计算符号值：1（正数）、0（0）、-1（负数）
ceil	向上取整（大于等于该值的最小整数）如：3.5取为4
floor	向下取整（小于等于该值的最小整数）如：3.5取为3
rint	将元素保留到整数位，并保持dtype
modf	分别将数组的小数部分和整数部分按数组形式返回
isnan	返回一个布尔类型数组判断元素是否为NaN（不是一个数值）数值会显示False
isfinite isinf	返回一个布尔类型数组分别判断元素是否有限（非inf 非NaN）、无限

5.2 二元通用函数

下述函数的调用方式全部为 np.函数名（arr1，arr2）

二元函数	描述
add multiply divide floor_divide mod	数组对应元素相加、相乘、除、整除（放弃余数）、求模
subtracrt	在arr2中，去除arr1包含的元素
power	将arr2的元素作为arr1对应元素的幂次方
fmax fmin	逐个元素计算最大（小）值、忽略NaN
greater greater_equal less less_equal equal not_equal	逐个元素进行比较，返回布尔数组（分别表示 >、>=、<、<=、==、!=）
logical_and logical_or logical_xor	逐个元素进行逻辑操作（与&、\|、^效果一致）