详细图解,二叉排序树的遍历、删除、插入,通过bf优化构建成平衡二叉树(avl树)的原理
目录
一.二叉排序树的建立
1.数据结构定义
class TreeNode
{
public:
int m_data = 0; //数据
TreeNode* m_lch = NULL; //左节点
TreeNode* m_rch = NULL; //右节点
TreeNode* m_father = NULL; //父亲节点
};
class Tree
{
public:
void PreOrderVisit(TreeNode* node); //前序遍历
void InOrderVisit(TreeNode* node); //中序遍历
void PostOrderVisit(TreeNode* node);//后序遍历
void InitTree(int* pArr, int n );
private:
void AddChild(TreeNode* TT, TreeNode* node);
TreeNode* m_root = NULL;
}下图展示了数据10,7,20,3,1,5,17构建一个有序二叉树的过程。
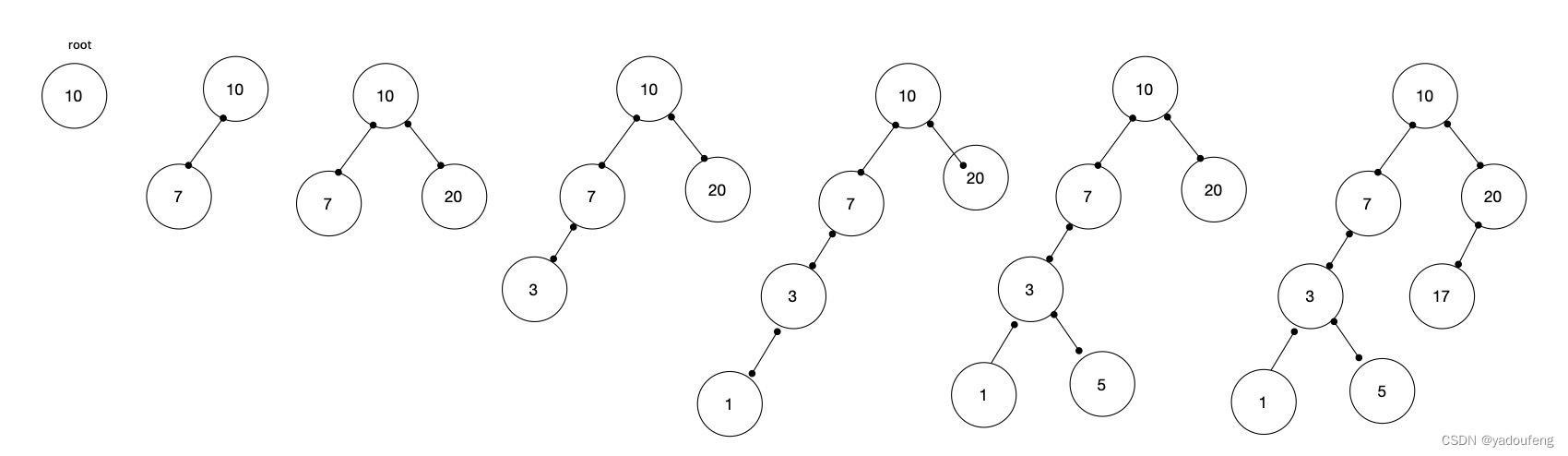
1.当树为空时,第一个数据设置为root。
2.新加入的数据如果比root小,root的左孩子为空,就加到root的左孩子节点。
3.新加入的数据如果比root大,root的右孩子为空,就加到root的右孩子节点。
4.如果新加入的数据比root小,且root的左孩子不为空,那把root的左孩子当作新ROOT,重复2,3,4,5步骤。
5.如果新加入的数据比root大,且root的右孩子不为空,那把root的右孩子当作新的ROOT,重复2,3,4,5步骤。
void AddChild(TreeNode* TT, TreeNode* node)
{
if(m_root == NULL)
{
m_root = node;
return ;
}
int cmp = node->m_data < TT->m_data;
if(cmp > 0) //如果数据比TT节点小,就找TT节点的左孩子比较
{
if(TT->m_lch == NULL)
{
SetLChild(TT, node);
return;
}
else //如果左节点不为空,递归到左节点
{
AddChild(TT->m_lch, node);
return;
}
}
else //如果数据比TT节点大,就找TT节点的右孩子比较
{
if(TT->m_rch == NULL)
{
SetRChild(TT, node);
return;
}
else //如果右节点不为空,递归到左节点
{
AddChild(TT->m_rch, node);
return;
}
}
}
void SetLChild(TreeNode* node, TreeNode* L)
{
if(node == NULL)
return;
node->m_lch = L;
if(L)
L->m_father = node;
}
void SetRChild(TreeNode* node, TreeNode* R)
{
if(node == NULL)
return;
node->m_rch = R;
if(R)
R->m_father = node;
}二.二叉树的遍历
二叉树的遍历是指从根节点出发,按照某种次序依次访问二叉树中所有节点,使得每个节点被访问一次且仅被访问一次。根据根节点的访问顺序有以下三种方式。
前序遍历,先访问根节点,再遍历左孩子,再遍历右孩子。上图访问顺序10 7 3 1 5 20 17
中序遍历,先中序遍历自己的左子树,再访问根节点,然后中序遍历自己右子树。上图访问顺序1 3 5 7 10 17 20
后序遍历,先后序遍历自己的左子树,再后序遍历自己的右子树,再访问根节点。上图访问顺序1 5 3 7 17 20 10
很显然一棵有序二叉树,用中序遍历就能按数据大小顺序依次输出。
代码利用递归方法实现很简单。
void PreOrderVisit(TreeNode* node)
{
if(node == NULL)
return;
cout << node->m_data << " ";
PreOrderVisit(node->m_lch);
PreOrderVisit(node->m_rch);
}
void InOrderVisit(TreeNode* node)
{
if(node == NULL)
return;
InOrderVisit(node->m_lch);
cout << node->m_data << " ";
InOrderVisit(node->m_rch);
}
void PostOrderVisit(TreeNode* node)
{
if(node == NULL)
return;
PostOrderVisit(node->m_lch);
PostOrderVisit(node->m_rch);
cout << node->m_data << " ";
}三.改造树结构
1.上述树节点存储的是int类型数据,我们使用模版TreeNode<T>使其能存储各种类型数据。
2.上述树默认是根据int类型数据升序排序,构建的有序二叉树。我们改造成能自定义排序使用升序还是降序,如果是存储自定义数据结构的,还可以自定义比较函数。
3.把树的遍历(打印输出),改成自定义方法。
四.有序二叉树的查找
根据比较函数和排序顺序,选择左子树或者右子树进行递归遍历查找。
TreeNode<T>* FindTreeNode(TreeNode<T>* node, T data, int sort(T, T)=NULL)
{
if(node == NULL)
return NULL;
else if(node->m_data == data)
return node;
int cmp = 0;
if(sort!=NULL)
cmp = sort(data, node->m_data);
else
cmp = data - node->m_data;
if(m_ascendorder)
{
if(cmp >= 0)
return FindTreeNode(node->m_rch, data);
else
return FindTreeNode(node->m_lch, data);
}
else
{
if(cmp >= 0)
return FindTreeNode(node->m_lch, data);
else
return FindTreeNode(node->m_rch, data);
}
return NULL;
}五.二叉排序树的节点删除
1.对于删除只有左子树或者右子树的节点,那很简单只需要子承父业就行。
2.对于删除即有左子树又有右子树的节点,那就不太容易了,比如下图。
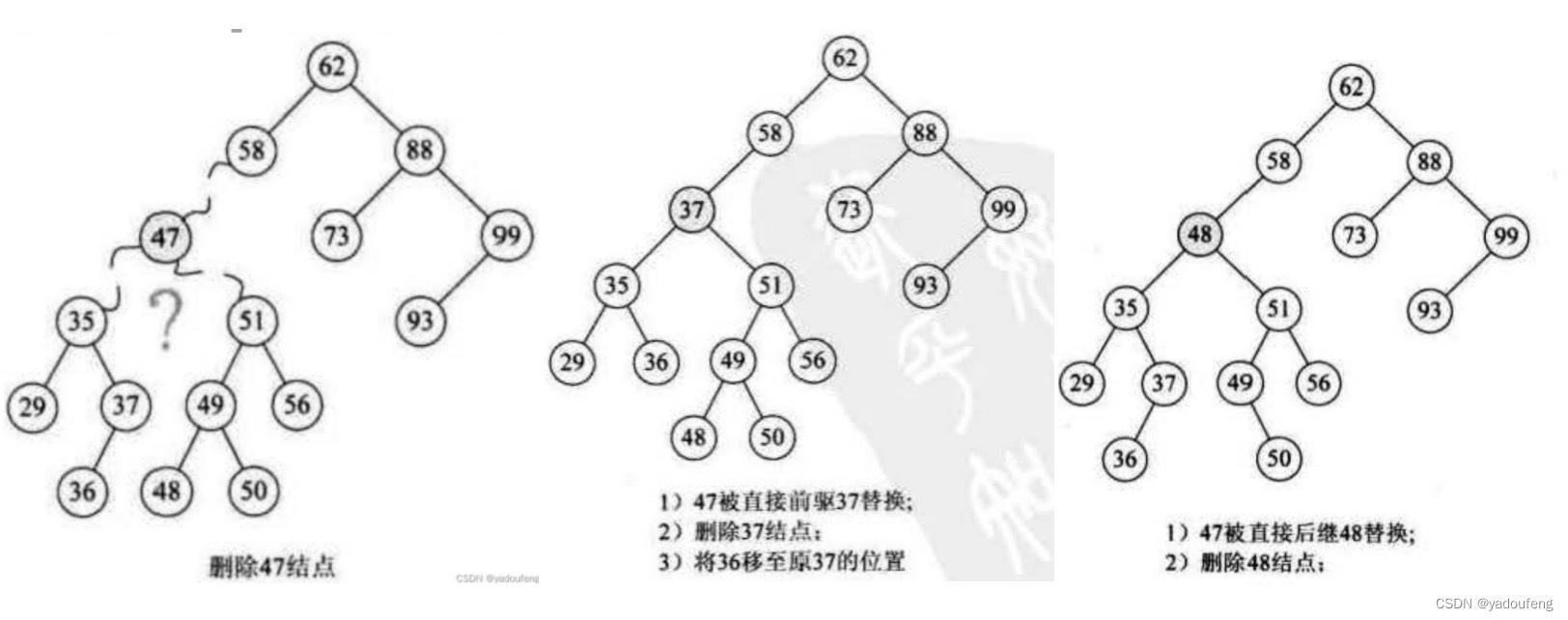
上面的中序遍历是29,35,36,37,47,48,49,50,51,56,58....... ,我们可以用47的前驱节点37,或者使用后驱节点48替换47的位置。
分析使用前驱节点替换方法:
1.先找到前驱节点,即删除节点的第一个左孩子的最后一个右孩子。为37,设为pre。
2.删除节点的右子树51,成为pre的右子树。
3.pre的左子树36,过继给pre的父节点35,成为35的右子树。
4.被删节点的第一个左节点35,成为pre的左孩子。
5.删除节点47(node)。把node替换成pre
//删除节点,使用前驱节点替换方法
//1.对于删除的节点,只有左孩子或右孩子时,很简单直接子承父业就行。
//2.如果被删除的节点即有左孩子,又有右孩子,可以使用前驱节点替换方法,或者使用后驱节点替换方法。
void DelTreeNode(TreeNode<T>* node)
{
if(node == NULL)
return;
if(node != m_root)
{
TreeNode<T>** pfatherchild;
if(node->m_father->m_lch == node)
pfatherchild = &node->m_father->m_lch;
else
pfatherchild = &node->m_father->m_rch;
if(node->m_lch == NULL)//只有右支,子承父业
{
*pfatherchild = node->m_rch;
if(node->m_rch)
node->m_rch->m_father = node->m_father;
}
else if(node->m_rch == NULL)//只有左支,子承父业
{
*pfatherchild = node->m_lch;
if(node->m_lch)
node->m_lch->m_father = node->m_father;
}
else//即有左支,又有右支,使用中序遍历时的前驱节点替换
{
//第1步,找到删除节点的第一个左孩子的最右孩子,是中序遍历时node的前驱节点。
TreeNode<T>* pre = node->m_lch;
while (pre->m_rch)
pre = pre->m_rch;
//第2步,被删除节点的右支过继到pre的右孩子。
SetRChild(pre, node->m_rch);
if(pre == pre->m_father->m_rch)
{
//第3步,pre节点的左支过继给pre节点的父节点
SetRChild(pre->m_father, pre->m_lch);
//第4步,被删节点的第一个左节点,成为pre的左孩子
SetLChild(pre, node->m_lch);
}
//第4步,node替换成pre节点
{
*pfatherchild = pre;
pre->m_father = node->m_father;
}
}
}
else //同样的方法对node==root时的特殊处理
{
TreeNode<T>* pre = m_root->m_lch; //找到删除节点的第一个左孩子
if(pre)
{
while (pre->m_rch)
pre = pre->m_rch;//第一个左孩子的最右孩子,就是中序遍历时node的前驱节点。
if(pre == pre->m_father->m_rch)
{
SetRChild(pre->m_father, pre->m_lch);
SetLChild(pre, node->m_lch);
}
SetRChild(pre , node->m_rch);
m_root = pre;
m_root->m_father = NULL;
}
else //删除的是根节点,且根节点没有左子树的情况
{
m_root = m_root->m_rch;
if(m_root)
m_root->m_father = NULL;
}
}
delete node;
}六.二叉排序树优化成平衡二叉树
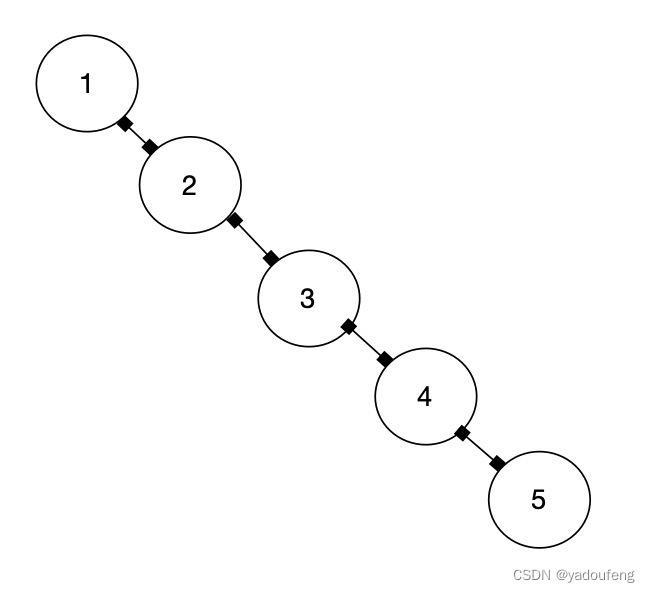
如果插入的数据顺序是1,2,3,4,5那么根据二叉排序树的建立过程,最后的树会是下图所示。此时查找5的话,需要遍历所有节点。为了提高查找效率,需要是它变成平衡二叉树,这样查找时间复杂度能变成O(log2N)
七.平衡二叉树的建立过程
1.平衡二叉树的特点
⑴:左子树和右子树深度之差的绝对值不大于1;
⑵:左子树和右子树也都是平衡二叉树。
平衡因子BF(Balance Factor) :二叉树上结点的左子树的深度减去其右子树深度称为该结点的平衡因子,因此平衡二叉树上每个结点的平衡因子只可能是-1、0和1
2.平衡二叉树,插入时平衡原理
在二叉排序树建立的基础上,每当插入一个新数据,计算各节点的平衡因子,如果绝对值大于1,就旋转使子树平衡。
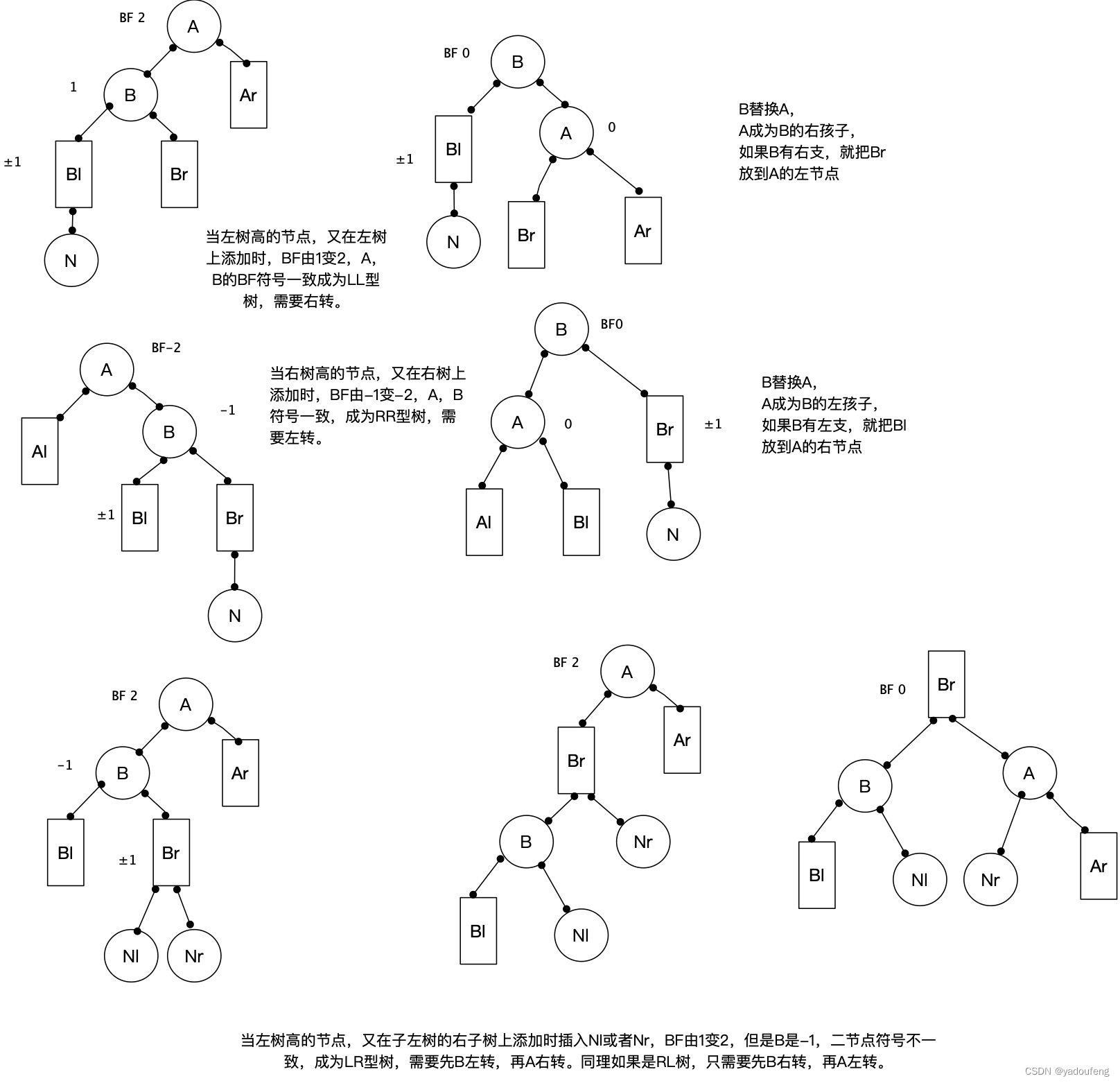
3.代码实现LL型,RR型,LR型,RL型树的旋转平衡
//左左型树旋转,往右旋转
void Rotate_LL(TreeNode<T>* root)
{
TreeNode<T>* rootf = root->m_father;
TreeNode<T>* node = root->m_lch;
if(rootf)
{
if(rootf->m_lch == root)
SetLChild(rootf, node);
else
SetRChild(rootf, node);
}
else
{
m_root = node;
m_root->m_father = NULL;
}
SetLChild(root, node->m_rch);
SetRChild(node, root);
}
//右右型树旋转,往左旋转
void Rotate_RR(TreeNode<T>* root)
{
TreeNode<T>* rootf = root->m_father;
TreeNode<T>* node = root->m_rch;
if(rootf)
{
if(rootf->m_lch == root)
SetLChild(rootf, node);
else
SetRChild(rootf, node);
}
else
{
m_root = node;
m_root->m_father = NULL;
}
SetRChild(root, node->m_lch);
SetLChild(node, root);
}
//左右型树旋转
void Rotate_LR(TreeNode<T>* root)
{
Rotate_RR(root->m_lch);
Rotate_LL(root);
}
//右左型树旋转
void Rotate_RL(TreeNode<T>* root)
{
Rotate_LL(root->m_rch);
Rotate_RR(root);
}4.旋转后BF值的更新
当时LL型或者RR型树,旋转平衡后,TT,L的BF都变为0。当LR型树,旋转平衡后,根据原树的Lr的BF值0,1,-1这3种情况,有三种结果。RL型树同理LR树。
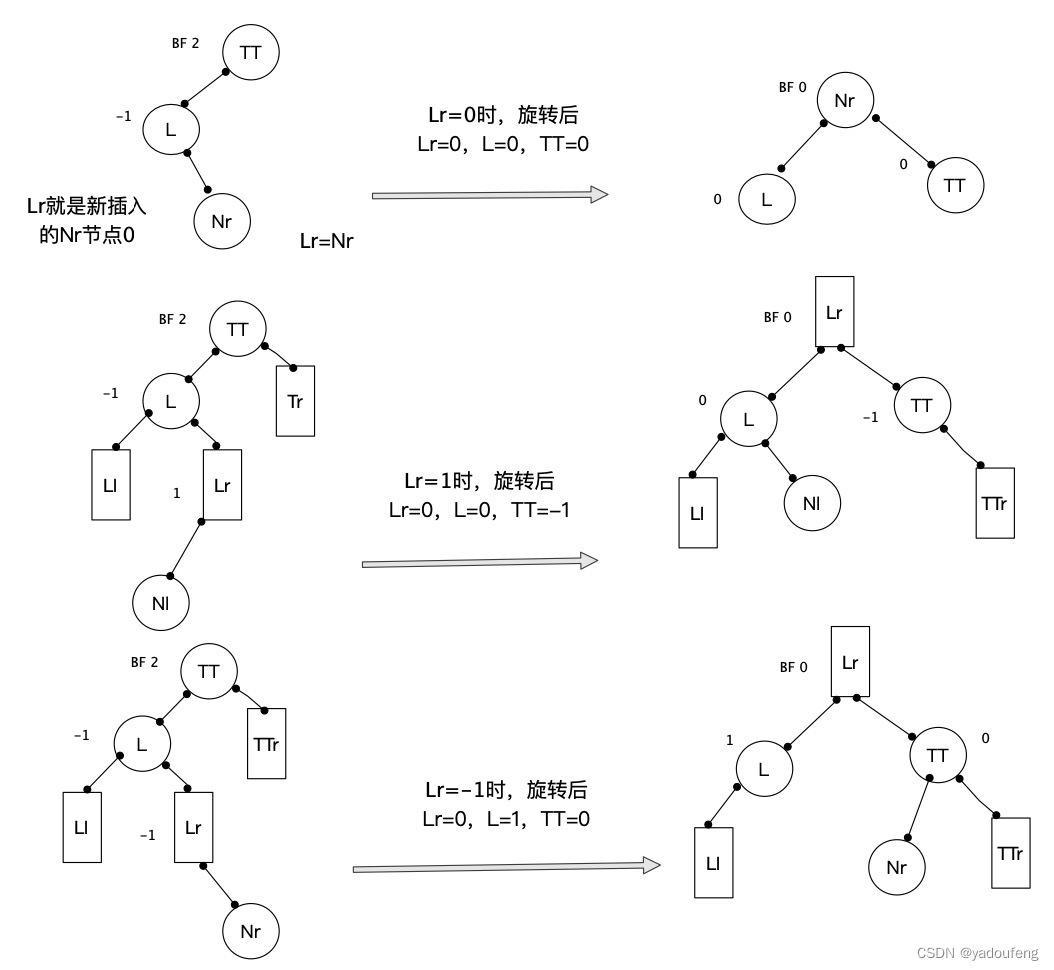
代码实现
void LeftBalance(TreeNode<T>* TT)
{
assert(TT->m_bf == TreeLH);
TreeNode<T>* L = TT->m_lch;
if(L->m_bf == TreeLH) // LL型树,插在树root的左孩子的左边
{
TT->m_bf = TreeEH;
L->m_bf = TreeEH;
Rotate_LL(TT);
}
else if(L->m_bf == TreeRH) //LR型树,插在树root的左孩子的右边,双旋处理
{
TreeNode<T>* lr = L->m_rch;
if(lr->m_bf == TreeLH)
{
TT->m_bf = TreeRH;
L->m_bf = TreeEH;
}
else if(lr->m_bf == TreeEH)
{
TT->m_bf = TreeEH;
L->m_bf = TreeEH;
}
else if(lr->m_bf == TreeRH)//
{
TT->m_bf = TreeEH;
L->m_bf = TreeLH;
}
lr->m_bf = TreeEH;
Rotate_LR(TT);
}
else
assert(false);
}八.总结
学习二叉树前需要熟练掌握递归。平衡二叉树的删除,和插入旋转是难点。但是只要多画图,根据图写代码还是容易分析的。指针指来指去的可能会懵圈,多些assert,自检下。
附上所有源码
#include "utility.h"
template <typename T>
class TreeNode
{
public:
T m_data = 0; //可以存储自定义的数据结构的数据
char m_bf = 0; //平衡二叉树每个节点的平衡因子,只能为 -1,0,1.
int m_depth = -1; //节点所在的深度
TreeNode* m_lch = NULL;
TreeNode* m_rch = NULL;
TreeNode* m_father = NULL;
};
template<typename T>
using dealTreeNode = void (*)(TreeNode<T>* node);
template <typename T>
class Tree
{
public:
~Tree()
{
PostOrderVisit(m_root, [](TreeNode<T>* node){ //通过传人自定义遍历函数,释放所有节点。
delete node;
});
}
//获取树的深度
int GetTreeDepth()
{
if(m_root == NULL)
return 0;
return GetDepth(m_root);
}
//删除节点,使用前驱节点替换方法
//1.对于删除的节点,只有左孩子或右孩子时,很简单直接子承父业就行。
//2.如果被删除的节点即有左孩子,又有右孩子,可以使用前驱节点替换方法,或者使用后驱节点替换方法。
void DelTreeNode(TreeNode<T>* node)
{
if(node == NULL)
return;
if(node != m_root)
{
TreeNode<T>** pfatherchild;
if(node->m_father->m_lch == node)
pfatherchild = &node->m_father->m_lch;
else
pfatherchild = &node->m_father->m_rch;
if(node->m_lch == NULL)//只有右支,子承父业
{
*pfatherchild = node->m_rch;
if(node->m_rch)
node->m_rch->m_father = node->m_father;
}
else if(node->m_rch == NULL)//只有左支,子承父业
{
*pfatherchild = node->m_lch;
if(node->m_lch)
node->m_lch->m_father = node->m_father;
}
else//即有左支,又有右支,使用中序遍历时的前驱节点替换
{
//第1步,找到删除节点的第一个左孩子的最右孩子,是中序遍历时node的前驱节点。
TreeNode<T>* pre = node->m_lch;
while (pre->m_rch)
pre = pre->m_rch;
//第2步,被删除节点的右支过继到pre的右孩子。
SetRChild(pre, node->m_rch);
if(pre == pre->m_father->m_rch)
{
//第3步,pre节点的左支过继给pre节点的父节点
SetRChild(pre->m_father, pre->m_lch);
//第4步,被删节点的第一个左节点,成为pre的左孩子
SetLChild(pre, node->m_lch);
}
//第4步,node替换成pre节点
{
*pfatherchild = pre;
pre->m_father = node->m_father;
}
}
}
else //同样的方法对node==root时的特殊处理
{
TreeNode<T>* pre = m_root->m_lch; //找到删除节点的第一个左孩子
if(pre)
{
while (pre->m_rch)
pre = pre->m_rch;//第一个左孩子的最右孩子,就是中序遍历时node的前驱节点。
if(pre == pre->m_father->m_rch)
{
SetRChild(pre->m_father, pre->m_lch);
SetLChild(pre, node->m_lch);
}
SetRChild(pre , node->m_rch);
m_root = pre;
m_root->m_father = NULL;
}
else //删除的是根节点,且根节点没有左子树的情况
{
m_root = m_root->m_rch;
if(m_root)
m_root->m_father = NULL;
}
}
delete node;
}
void InitTree(int* pArr, int n , int sort(const T, const T) = NULL)
{
for(int i = 0; i < n; i++)
{
TreeNode<T>* node = new TreeNode<T>();
node->m_data = pArr[i];
if(m_bavl)
AVLAddChild(m_root, node, sort);
else
AddChild(m_root, node, sort);
}
}
void InitAVLTree(int* pArr, int n, int sort(const T, const T) = NULL)
{
m_bavl = true;
InitTree(pArr, n, sort);
}
TreeNode<T>* FindTreeNode(T data, int sort(T, T) = NULL)
{
return FindTreeNode(m_root, data, sort);
}
void PreOrderVisit(dealTreeNode<T> fun)
{
PreOrderVisit(m_root, fun);
}
void InOrderVisit(dealTreeNode<T> fun)
{
InOrderVisit(m_root, fun);
}
void PostOrderVisit(dealTreeNode<T> fun)
{
PostOrderVisit(m_root, fun);
}
private:
int GetDepth(TreeNode<T>* node)
{
if(node == NULL)
return 0;
node->m_depth = max(GetDepth(node->m_lch), GetDepth(node->m_rch)) + 1;
return node->m_depth;
}
TreeNode<T>* FindTreeNode(TreeNode<T>* node, T data, int sort(T, T)=NULL)
{
if(node == NULL)
return NULL;
else if(node->m_data == data)
return node;
int cmp = 0;
if(sort!=NULL)
cmp = sort(data, node->m_data);
else
cmp = data - node->m_data;
if(m_ascendorder)
{
if(cmp >= 0)
return FindTreeNode(node->m_rch, data);
else
return FindTreeNode(node->m_lch, data);
}
else
{
if(cmp >= 0)
return FindTreeNode(node->m_lch, data);
else
return FindTreeNode(node->m_rch, data);
}
return NULL;
}
void LeftBalance(TreeNode<T>* TT)
{
assert(TT->m_bf == TreeLH);
TreeNode<T>* L = TT->m_lch;
if(L->m_bf == TreeLH) // LL型树,插在树root的左孩子的左边
{
TT->m_bf = TreeEH;
L->m_bf = TreeEH;
Rotate_LL(TT);
}
else if(L->m_bf == TreeRH) //LR型树,插在树root的左孩子的右边,双旋处理
{
TreeNode<T>* lr = L->m_rch;
if(lr->m_bf == TreeLH)
{
TT->m_bf = TreeRH;
L->m_bf = TreeEH;
}
else if(lr->m_bf == TreeEH)
{
TT->m_bf = TreeEH;
L->m_bf = TreeEH;
}
else if(lr->m_bf == TreeRH)//
{
TT->m_bf = TreeEH;
L->m_bf = TreeLH;
}
lr->m_bf = TreeEH;
Rotate_LR(TT);
}
else
assert(false);
}
void RightBalance(TreeNode<T>* TT)
{
assert(TT->m_bf == TreeRH);
TreeNode<T>* R = TT->m_rch;
if(R->m_bf == TreeRH) //RR型树, 插在树root的右孩子的右边
{
TT->m_bf = TreeEH;
R->m_bf = TreeEH;
Rotate_RR(TT);
}
else if(R->m_bf == TreeLH)//RL型树,插在树root的右孩子的左边,双旋处理
{
TreeNode<T>* rl = R->m_lch;
if(rl->m_bf == TreeLH)
{
TT->m_bf =TreeEH;
R->m_bf = TreeRH;
}
else if(rl->m_bf == TreeEH)
{
TT->m_bf = TreeEH;
R->m_bf = TreeEH;
}
else if(rl->m_bf == TreeRH)
{
TT->m_bf = TreeLH;
R->m_bf = TreeEH;
}
rl->m_bf = TreeEH;
Rotate_RL(TT);
}
else
assert(false);
}
void AddChild(TreeNode<T>* TT, TreeNode<T>* node, int sort(T, T))
{
if(m_root == NULL)
{
m_root = node;
return ;
}
int cmp = 0;
if(sort)
cmp = sort(node->m_data, TT->m_data);
else
cmp = node->m_data < TT->m_data;
if((m_ascendorder && cmp > 0) || (!m_ascendorder && cmp < 0))
{
if(TT->m_lch == NULL)
{
SetLChild(TT, node);
return;
}
else
{
AddChild(TT->m_lch, node, sort);
return;
}
}
else
{
if(TT->m_rch == NULL)
{
SetRChild(TT, node);
return;
}
else
{
AddChild(TT->m_rch, node, sort);
return;
}
}
assert(false);
}
//返回值是,TT的深度增加值
int AVLAddChild(TreeNode<T>* TT, TreeNode<T>* node, int sort(T, T))
{
if(m_root == NULL)
{
m_root = node;
m_root->m_bf = TreeEH;
return 1;
}
int cmp = 0;
if(sort)
cmp = sort(node->m_data, TT->m_data);
else
cmp = node->m_data < TT->m_data;
if((m_ascendorder && cmp > 0) || (!m_ascendorder && cmp < 0))
{
if(TT->m_lch == NULL)
{
SetLChild(TT, node);
node->m_bf = TreeEH;
if(TT->m_rch == NULL)
{
assert(TT->m_bf == TreeEH);
TT->m_bf = TreeLH;
return 1;
}
else
{
assert(TT->m_bf == TreeRH);
TT->m_bf = TreeEH;
return 0;
}
}
else
{
int ret = AVLAddChild(TT->m_lch, node, sort);
if(ret) // 插入结果:TT的左树增加一层。
{
if(TT->m_bf == TreeLH)//TT本来就左树高,又在TT的左树增加1层。
{
LeftBalance(TT);
return 0;
}
else if(TT->m_bf == TreeEH)
{
TT->m_bf = TreeLH;
return 1;
}
else if(TT->m_bf == TreeRH)
{
TT->m_bf = TreeEH;
return 0;
}
}
else
return ret; //equal return 0;
}
}
else
{
if(TT->m_rch == NULL)
{
SetRChild(TT, node);
node->m_bf = TreeEH;
if(TT->m_lch == NULL)
{
assert(TT->m_bf == TreeEH);
TT->m_bf = TreeRH;
return 1;
}
else
{
assert(TT->m_bf==TreeLH);
TT->m_bf = TreeEH;
return 0;
}
}
else
{
int ret = AVLAddChild(TT->m_rch, node, sort);
if(ret)//插入结果:TT的右树增加一层。
{
if(TT->m_bf == TreeRH) //TT的右树高,又在右树上加一成
{
RightBalance(TT);
return 0;
}
else if(TT->m_bf == TreeEH)
{
TT->m_bf = TreeRH;
return 1;
}
else if(TT->m_bf == TreeLH)
{
TT->m_bf = TreeEH;
return 0;
}
}
else
return ret;
}
}
assert(false);
}
//前序遍历,每个节点使用函数fun访问
void PreOrderVisit(TreeNode<T>* node, dealTreeNode<T> fun)
{
if(node == NULL)
return;
if(fun!=NULL)
fun(node);
PreOrderVisit(node->m_lch, fun);
PreOrderVisit(node->m_rch, fun);
}
//中序遍历,每个节点使用函数fun访问
void InOrderVisit(TreeNode<T>* node, dealTreeNode<T> fun)
{
if(node == NULL)
return;
InOrderVisit(node->m_lch, fun);
if(fun!=NULL)
fun(node);
#ifdef DEBUG //for check
{
if(node->m_father!=NULL)
{
if(node!=m_root)
{
assert(node->m_father);
assert(node->m_father != node);
assert(node->m_lch!=node);
assert(node->m_rch!=node);
assert(node->m_father!=node->m_lch);
assert(node->m_father!=node->m_rch);
}
else
{
assert(node->m_father == NULL);
assert(node->m_lch!=node);
assert(node->m_rch!=node);
}
}
if(node->m_lch)
assert(node->m_lch->m_father==node);
if(node->m_rch)
assert(node->m_rch->m_father==node);
}
#endif
InOrderVisit(node->m_rch, fun);
}
//后序遍历,每个节点使用函数fun访问
void PostOrderVisit(TreeNode<T>* node, dealTreeNode<T> fun)
{
if(node == NULL)
return;
PostOrderVisit(node->m_lch, fun);
PostOrderVisit(node->m_rch, fun);
if(fun!=NULL)
fun(node);
}
//把L设置成node的左孩子
void SetLChild(TreeNode<T>* node, TreeNode<T>* L)
{
if(node == NULL)
return;
node->m_lch = L;
if(L)
L->m_father = node;
}
//把R设置成node的右孩子
void SetRChild(TreeNode<T>* node, TreeNode<T>* R)
{
if(node == NULL)
return;
node->m_rch = R;
if(R)
R->m_father = node;
}
//左左型树旋转,往右旋转
void Rotate_LL(TreeNode<T>* root)
{
TreeNode<T>* rootf = root->m_father;
TreeNode<T>* node = root->m_lch;
if(rootf)
{
if(rootf->m_lch == root)
SetLChild(rootf, node);
else
SetRChild(rootf, node);
}
else
{
m_root = node;
m_root->m_father = NULL;
}
SetLChild(root, node->m_rch);
SetRChild(node, root);
}
//右右型树旋转,往左旋转
void Rotate_RR(TreeNode<T>* root)
{
TreeNode<T>* rootf = root->m_father;
TreeNode<T>* node = root->m_rch;
if(rootf)
{
if(rootf->m_lch == root)
SetLChild(rootf, node);
else
SetRChild(rootf, node);
}
else
{
m_root = node;
m_root->m_father = NULL;
}
SetRChild(root, node->m_lch);
SetLChild(node, root);
}
//左右型树旋转
void Rotate_LR(TreeNode<T>* root)
{
Rotate_RR(root->m_lch);
Rotate_LL(root);
}
//右左型树旋转
void Rotate_RL(TreeNode<T>* root)
{
Rotate_LL(root->m_rch);
Rotate_RR(root);
}
TreeNode<T>* m_root = NULL;
bool m_ascendorder = true; //是否升序排序
bool m_bavl = false; //是否是平衡二叉树
const static int TreeLH = 1;//左子树比右子树深度大1.
const static int TreeEH = 0;//左子树和右子树深度一样.
const static int TreeRH = -1;//右子树和子子树深度一样.
};
int main()
{
vector<int > v;
int arr[] = {62,188,58,47,0,2,35,432,431,430,444,455,73,6,7,51,-10,1,99,37,828,88,93};
static int allsum = 0;
for(int i = 0 ; i < arraysize(arr); ++i)
{
Tree<double> tree;
tree.InitTree(arr, arraysize(arr));
tree.DelTreeNode(tree.FindTreeNode(arr[i]));
tree.InOrderVisit([](TreeNode<double>* node){
cout << node->m_data << " ";
allsum += node->m_data;
});
cout << endl;
}
int sum = 0;
for(int i = 0; i <arraysize(arr); ++i)
sum+=arr[i];
assert(allsum/sum == arraysize(arr) -1);
cout << endl << endl;
int avltreedepth = 0;
for(int i = 0 ; i < arraysize(arr); ++i)
{
Tree<double> tree;
tree.InitAVLTree(arr, arraysize(arr));
tree.DelTreeNode(tree.FindTreeNode(arr[i]));
tree.InOrderVisit([](TreeNode<double>* node){
cout << node->m_data << " ";
allsum += node->m_data;
});
cout << endl;
}
cout << endl;
int arr1[] = {1,2,3,4,5,6,7,8};
Tree<double> tree;
tree.InitTree(arr1, arraysize(arr1));
Tree<double> tree1;
tree1.InitAVLTree(arr1, arraysize(arr1));
cout << "tree depth:" << tree.GetTreeDepth() << " AVLtree depth:" << tree1.GetTreeDepth() << endl;
return 0;
}