【探讨】bp神经网络是前馈还是后馈
目录
本文部分图文代码借鉴《老饼讲解-BP神经网络》
一、BP神经网络简介
1.1 什么是BP神经网络
BP神经网络也称为误差反向传播神经网络,是1986年由Rumelhart和McClelland为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,是应用最广泛的神经网络模型之一。
BP算法的基本思想是通过将输入样本输入网络中,然后将网络的输出与目标输出进行比较,计算误差,并将误差进行反向传播,以更新网络的权重。反向传播过程中,误差被分配给前一层的神经元,以及与神经元之间的连接权重,然后根据误差大小调整权重值。这个过程不断重复,直到网络的输出与目标输出接近。
BP神经网络具有任意复杂的模式分类能力和优良的多维函数映射能力,解决了简单感知器不能解决的异或和一些其他问题。BP算法的优点是可以对复杂的非线性问题进行建模,并且可以通过调整网络结构和参数来改进模型的性能。但它也存在一些问题,比如容易陷入局部最小值,并且计算量较大。
总的来说,BP算法是人工神经网络中最常用的训练算法之一,可以用来解决各种问题,包括分类、回归和模式识别等。
1.2 BP神经网络的结构
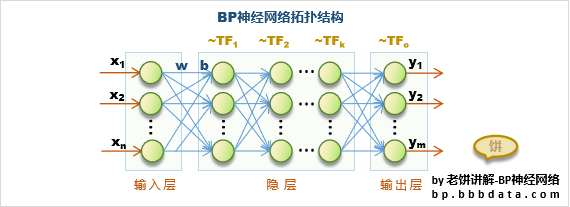
BP神经网络由输入层、隐藏层和输出层组成,其中隐藏层可以包含多个神经元。它的训练过程可以分为前向传播和误差反向传播两个阶段。在前向传播阶段,输入数据经过权重和偏置的变换后,经过激活函数处理后传递到下一层,最终产生输出。在误差反向传播阶段,根据实际输出与目标输出的误差计算损失函数,并通过反向传播算法计算各层的误差,再利用梯度下降算法调整各层之间的权重和偏置,以使损失函数最小化。
二、BP神经网络的前馈与后馈
2.1 什么是BP神经网络的前馈
BP神经网络的前馈是指信息从网络的输入层传递到输出层的过程。在前馈过程中,每个神经元将它的输入与相应的权重进行加权求和,并通过激活函数进行非线性变换处理,然后将结果传递给下一层的神经元,直到信息传递到输出层。
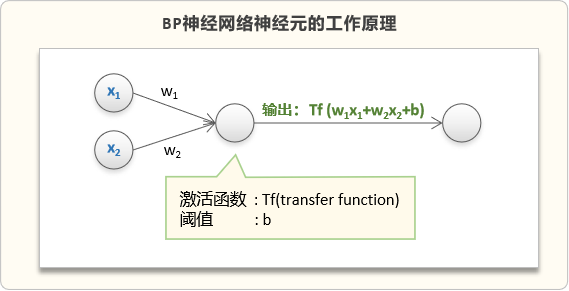
具体步骤如下:
1. 输入层接收外部的输入数据,并将数据传递到下一层隐藏层的神经元。
2. 隐藏层的神经元将输入与相应的权重进行加权求和,并通过激活函数进行非线性变换处理,然后将结果传递到下一层隐藏层的神经元。
3. 重复步骤2,直到信息传递到输出层的神经元。
4. 输出层的神经元将输入与相应的权重进行加权求和,并通过激活函数进行非线性变换处理,得到网络的输出结果。
在前馈过程中,每个神经元的输入值和输出值都会经过计算和传递,直到达到输出层产生最终的输出结果。这个过程是单向的,信息只能从输入层向输出层传递,没有反向传递。
总的来说,计算BP神经网络的输出时,BP神经网络是以前馈的方式计算得出网络的输出值,前馈往往指的就是BP神经网络计算输出的过程或方式。
2.2 什么是BP神经网络的后馈
BP,全称为"Backpropagation",翻译为中文就是”向后传播“,也就是通常所说的”后馈“,那么,后馈指的是什么呢?这就涉及到BP神经网络的训练算法。通常训练BP神经网络使用的是梯度下降等等之类的算法,由于BP神经网络的特殊结果,这类型的训练算法在训练权重阈值时是以反向传播误差的方式来更新神经网络的权重,以使网络能够逼近目标输出。
在BP神经网络中,首先使用随机初始化的权重参数进行前向传播,将输入样本通过网络的多层连接传递,经过激活函数的处理,得到输出结果。然后,将输出结果与标签进行比较,得到误差。接下来,将误差从输出层开始,按照权重的反向方向,通过链式法则将误差逐层传递回隐藏层和输入层。在传递过程中,根据误差值和梯度下降算法,更新连接权重和偏置,使得网络的输出逼近于目标输出。这个过程不断迭代,直到网络的输出与目标输出的误差达到预设的阈值或训练轮次达到预设的次数。
通过后馈过程,BP神经网络可以利用误差信号来调整网络参数,使网络能够自我学习和适应输入输出关系,从而提供更准确的预测和分类能力
三、BP神经网络前馈与后馈的关系
3.1 BP神经网络前馈与后馈的区别
BP神经网络的前馈与后馈的区别如下:
1.阶段不同:BP神经网络的前馈发生在网络输出的计算阶段,而BP神经网络的后馈过程发生在训练的阶段。
2.计算对象不同:BP神经网络的前馈计算的是BP神经网络神经元的值,而BP神经网络的后馈计算的是BP神经网络参数的梯度。
3.影响不同:BP神经网络的前馈影响的是网络的准确性,BP神经网络的后馈影响的是网络的训练。
3.2 BP神经网络前馈与后馈的意义
BP神经网络既有前馈,也有后馈,也即网络是前馈的,但训练是后馈的。
1.BP神经网络的前馈与后馈的意义
BP神经网络的前馈与后馈都给网络带来了极大的好处,它使得网络的计算和训练都不受层数的影响,只是类似套娃式一直向前或向后传播就可以。
2.BP神经网络训练中的前馈与后馈
比较需要注意的是,由于BP神经网络的梯度计算同时也依赖于神经元的值,所以往往在反馈之前 ,需要先前馈算出所有神经元的值,再进行后馈计算梯度,并更新权重阈值。
四、BP神经网络前馈与后馈-实例
在matlab中训练一个BP神经网络
x1 = [-3,-2.7,-2.4,-2.1,-1.8,-1.5,-1.2,-0.9,-0.6,-0.3,0,0.3,0.6,0.9,1.2,1.5,1.8]; % x1:x1 = -3:0.3:2;
x2 = [-2,-1.8,-1.6,-1.4,-1.2,-1,-0.8,-0.6,-0.4,-0.2,0,0.2,0.4,0.6,0.8,1,1.2]; % x2:x2 = -2:0.2:1.2;
y = [0.6589,0.2206,-0.1635,-0.4712,-0.6858,-0.7975,-0.8040,...
-0.7113,-0.5326,-0.2875 ,0,0.3035,0.5966,0.8553,1.0600,1.1975,1.2618]; % y: y = sin(x1)+0.2*x2.*x2;
inputData = [x1;x2]; % 将x1,x2作为输入数据
outputData = y; % 将y作为输出数据
setdemorandstream(88888); % 指定随机种子,这样每次训练出来的网络都一样。
%使用用输入输出数据(inputData、outputData)建立网络,
%隐节点个数设为3.其中隐层、输出层的传递函数分别为tansig和purelin,使用trainlm方法训练。
net = newff(inputData,outputData,3,{'tansig','purelin'},'trainlm');
%设置一些常用参数
net.trainparam.goal = 0.0001; % 训练目标:均方误差低于0.0001
net.trainparam.show = 400; % 每训练400次展示一次结果
net.trainparam.epochs = 15000; % 最大训练次数:15000.
[net,tr] = train(net,inputData,outputData); % 调用matlab神经网络工具箱自带的train函数训练网络
simout = sim(net,inputData); % 调用matlab神经网络工具箱自带的sim函数得到网络的预测值
figure; % 新建画图窗口窗口
t=1:length(simout);
plot(t,y,t,simout,'r') % 画图,对比原来的y和网络预测的y1. 运行过程如下:
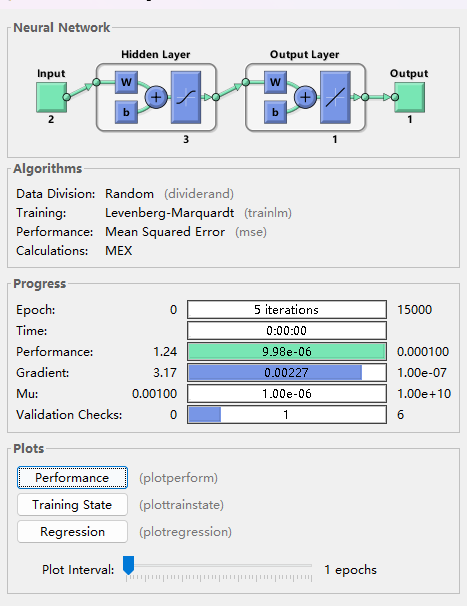
在这个训练过程中,就是通过BP神经网络的后馈进行训练的,当然,如上所述,在后馈之前也会先进行前馈来预计算各个神经元值。
2. 运行结果如下:
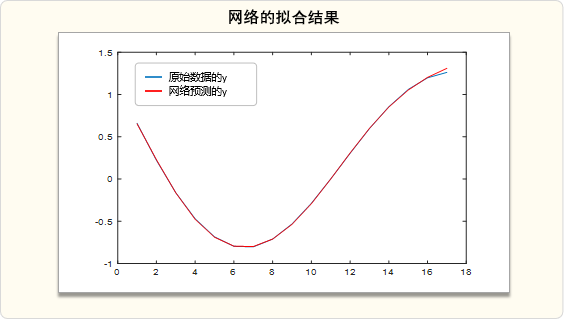
上图是网络的预测结果,可以看到,已经很好地拟合了原始数据点。
而BP神经网络的这个预测过程,就只涉及到BP神经网络的前馈。
如果觉得本文有帮助,点个赞吧!收个藏吧!