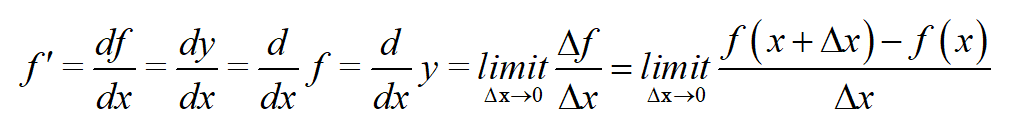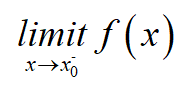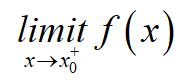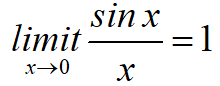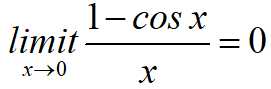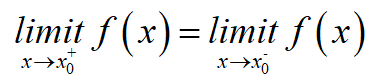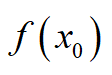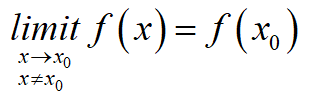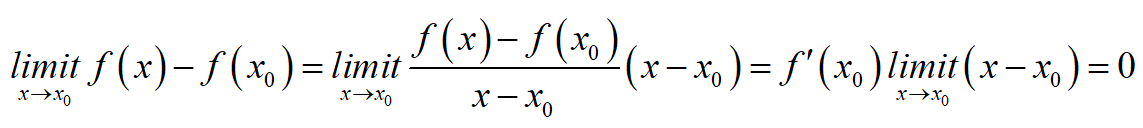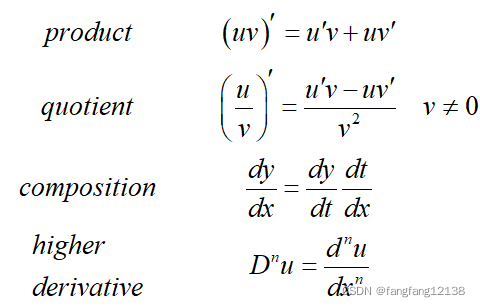微积分 Calculus 学习笔记（周更）

MIT公开课

学习目的：回顾相关知识点。

一、单变量微积分 One Variable Calculus

Part 1 导数 derivative

Unit1 导数 极限 连续

1 导数的一般定义

1. 单变量微积分并不指问题中变量唯一，而是求导的只对某一个变量
2. 几何解释：割线两点，固定一点，移动另一点，当两点无限接近时，割线即为切线，其斜率也即该点的导数
   

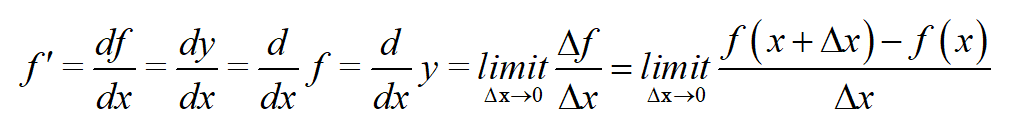
2 极限 limits

left-hand limit	right-hand limit

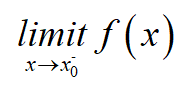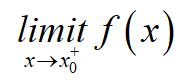特殊函数求极限

3 连续 continuity

1. 连续的条件

左右极限存在且相等	函数值存在	极限与函数值相等

2. 不连续的四种情况

跳跃间断 jump discontinuities	可去间断 removable discontinuities	无穷间断 infinite discontinuities	其他间断
典型的分段函数，左右极限不等	连续的曲线上，某点不存在，或不在线上	比如双曲线	振荡型的，如sin(1/x)

3. 可导必连续 differentable implies continuous
   f(x) is differentable at x₀ → f(x) is continuous at x₀
   

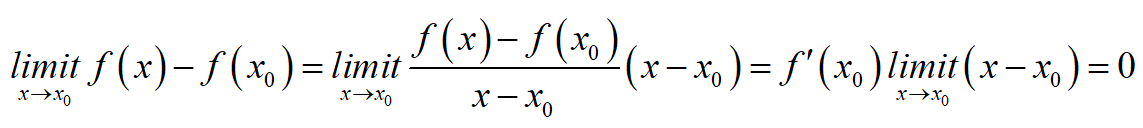
4 求导

1. sin/cos 在0点的导数推出了其他点的导数，指数函数也一样
2. 三角函数定理

sec²x=tan²x+1

3. 四则运算：C、±、×、÷、链式法则、高阶求导
   
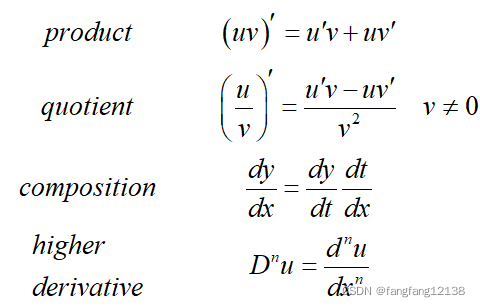
4. 重要的特殊函数求导

幂函数	(xn )’ = nxn-1
三角函数	(cosx)’ = -sinx	(sinx)’ = cosx	(tanx)’ = sec2x	(secx)’ = secx·tanx
反三角函数	(cos-1x)’ = -1/√(1 - x2)	(sin-1x)’ = 1/√(1 - x2)	(tan-1x)’ = 1/(1+x2)
指数函数	(ax )’ = ax lna	(ex )’ = ex
对数函数	(loga(x))’ = 1/(xlna)	(lnx )’ = 1/x

5. 对数微分法
   (lnu)’ = u’/u
   limit(n→∞)(1+1/n)ⁿ = e ≈ (1+1/100)¹⁰⁰ = 2.71828
6. 隐函数微分与反函数
   1. 无法给出或给出的解析式较为复杂，采用隐函数微分 implicit differentiation
   2. 举个栗子
      y⁴ + xy² - 2 = 0，等式两边同时微分，有，4y³ y’ + y² + x·2y·y’ = 0
   3. 反函数 inverse func
      y = f(x) ，x = g(y)，g(f(x)) = x，g = f^-1 ，f = g^-1
      举例：y = tan^-1 (x)，y = sin^-1 (x)，等，都可以通过先求反函数，然后通过隐函数微分进行求导

Unit2 导数的应用

1 线性近似

1. 一阶 f(x) ≈ f(x₀) + f’(x₀)(x - x₀)
2. 二阶 f(x) ≈ f(x₀) + f’(x₀)(x - x₀) + 0.5f’'(x₀)(x - x₀) ²
3. 曲线在切点处近似于切线，利用该性质，可以将复杂函数化简、求解函数值
4. 特别的，当 x₀ = 0 时，有 f(x) ≈ f(0) + f’(0)x ，f(x) ≈ f(0) + f’(0)x + 0.5f’'(0)x ²
5. 特殊函数在 x = 0 附件近似如下，注意换元

原函数	一阶近似	二阶近似
sinx	x	x
cosx	1	1 - 0.5x2
ex	1 + x	1 + x +0.5x2
ln(x + 1)	x	x - 0.5x2
(1 + x)r	1 + rx	1 + rx + 0.5r(r-1)x2

2 曲线构图

1. 极值点、驻点（f’ = 0）、拐点（f’’ = 0），驻点包含极值点
2. 凸 f’’ > 0，凹 f‘’ < 0
3. 最大值 最小值：驻点、ends pts、special

问题 环在绳上的位置

启示：斜拉桥 承重 角度相等 受力相同

3 牛顿迭代法

1. 不断迭代以找到解，基本迭代式如下，误差下降速度较快，但受限于很多条件。
2. x₁ = x₀ - f(x₀) / f’(x₀)
3. 应用条件：函数一阶导不能太小，特别是不为0；二阶导不能太大，二阶导为0可以得到准确解；x₀ 要接近想要的解，因为牛顿迭代可能会找到错误解。

4 中值定理 Mean Value Theorem

1. 基本公式为： ( f(b) - f(a) ) / ( b - a ) = f’(c ) 条件：a<c<b，f(x)在(a,b)内可导，在[a,b]上连续。
2. 变换为一般形式：f(b) = f(a) + f’(c )( b - a )
3. 区分 线性近似：线性近似是近似，约等于；中值定理是equal，明确相等。如平均速度，线性近似得到的结论是平均速度可以近似于初始速度或最终速度，中值定理可以知道平均速度的上下限。
4. 应用不等式证明 f’(c ) 恒> 0 则 函数递增， f’(c ) 恒< 0 则 函数递减， f’(c ) 恒= 0，常数。证明如 e^x > 1 + x + x² / 2! + x³ / 3! + x⁴ / 4! + …

Part 2 积分 integration

Unit3 微分 differentials

1 无穷小量与不定积分

1. 莱布尼茨微积分符号 dy dx 以及长S，比牛顿麻将式的无限加点要方便…
2. 无穷小量。
3. 不定积分。反导数（antiderivatives）←→ 不定积分（indefine integral）G(x) = ∫ g(x)dx，通俗一点就是G’(x) =g(x)。称其为不定积分，不定在于G(x)可以附加任意常数。
4. 积分的唯一性。 if G’ = F’，then G = F + const
5. 换元法求积分。∫(x⁴ + 2)⁴ x³ dx →→换元→ u = x⁴ + 2 , du = 4x³ dx →→→ ∫(x⁴ + 2)⁴ x³ dx = ∫ u⁴ 0.25du = 0.25 ∫ u⁴du →→还原

2 微分方程与分离变量

单词

1. U1
   单变量微积分 one variable calculus 微分 differentials 求导 differentiate 导数 derivative
   几何解释 geometry interpretation
   切线 tangent line 割线 secant line 斜率 slope
   差商 difference quotient
   瞬时的 instantaneous 梯度 gradient 奇函数/偶函数 odd/even func
   推算 deduce 不确定度 degree of uncertainly
   对消运算 cancellation
   公式 formula 分为两类 come in two flavors 指出 figure out 证明 proof
   阶乘 factorial
   技巧 technique 幂运算 exponent operator
   指数 exponentials 对数 logarithms 插值直到连续 filling in by continuity 对数微分法 logarithm differentiation 拓展 stretch
2. U2
   线性近似 linear approximations 二阶线性近似 quadratic approximation
   曲线构图 curve sketching 极值点 turning / extremum point
   驻点 critical / stationary point 拐点 inflection point
   凸 concave up / convex 凹 concave down / concave
   正比关系 notion of proportionality 无量纲 dimensionless quantity
   重申 reiterate
   平行线 parallel line 证明不成立 ruin the proof 不等式 inequality
3. U3
   无穷小量 infinitesimals 换元法 substitution